Подразделы
Другие разделы
| 2446. Сумма чисел |
| 2447. База данных |
| 2448. Декодирование Хаффмана |
| 2450. Список файлов в архиве |
Дата и время
12/03/2026 15:34:56
 2449. Кодирование Хаффмана
2449. Кодирование Хаффмана
 Кодирование Хаффмана
Кодирование Хаффмана
 Учебные задачи: бинарные файлы
Учебные задачи: бинарные файлы
| 01/09/2007 | Основы программирования. Бинарные файлы (4) |
Ограничения: время – 500ms/1000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
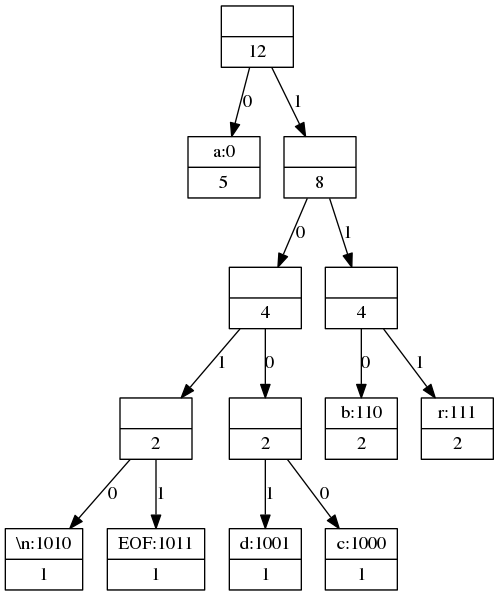
Ввод содержит некоторый текст до `10^6` символов. Закодировать этот текст с помощью кода Хаффмана.
Дерево кодирования строится следующим образом.
Для каждого символа текста, включая пробелы и переходы на новую строку,
подсчитывается количество его появлений в тексте.
Для всех символов, появляющихся в тексте хотя бы один раз, добавляется вершина.
Кроме того в набор вершин включается нулевой символ для конца текста с количеством появлений 1.
После этого выбирается две вершины с наименьшим количеством появлений и
они заменяются на одну вершину с количеством появлений, равным их сумме, а заменяемые вершины
становятся ее потомками.
Это действие выполняется до тех пор, пока не останется одна вершина.
Первая часть файла содержит структуру дерева кодирования.
Бит 1 указывает на лист дерева, далее следует 8 бит ASCII-кода, начиная со старшего.
Бит 0 указывает на промежуточный лист дерева, далее следует описание
левой ветки дерева, кодируемой битом 0, и правой ветки дерева, кодируемой битом 1.
Вторая часть файла содержит закодированный текст.
Коды символов задаются в файле, начиная со старшего бита, и
соответствуют пути от корня дерева до листа-символа.
Код для нулевого символа завершает вывод закодированного текста.
Неполный байт добавляется до полного произвольными битами и выводится.
Вывести в файл output.bin структуру дерева и закодированный текст.
Если существует несколько вариантов кодирования, то вывести любой из них.
Пример ввода
abracadabra
Бинарный файл output.bin
0й байт 1й байт 2й байт 3й байт 4й байт 5й байт 6й байт 7й байт 8й байт 0 123456701 2 3 4 567012345 670123456 7 012345670 123456701 2 345670123 456701234 0 101100001 0 0 0 101100011 101100100 0 100001010 100000000 0 101100010 101110010 a c d \n EOF b r 8й 9й байт 10й байт 11й байт 12й байт 5 670 123 4 5670 1 2345 6 701 234 5 6701 234567 0 110 111 0 1000 0 1001 0 110 111 0 1010 1011?? a b r a c a d a b r a \n EOF
 Рис. 1
Рис. 1


 Начало
Начало Учебные задачи
Учебные задачи