Задачи очного тура отборочных командных соревнований школьников

A. Музыкальные стулья

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Петя с друзьями играет в "Музыкальные стулья". Петя нашёл нотную запись мелодий, которые будут использованы в игре, и теперь хочет узнать их точную продолжительность.

Нота	Название	Обозначение во входных данных	Длительность в секундах при темпе 120BPM
	Бревис	0	4
	Целая	1	2
	Половинная	2	1
	Четверная	4	1/2
	Восьмая	8	1/4
	Шестнадцатая	16	1/8

Напишите программу, определяющую длительность мелодии в секундах.

Первая строка ввода содержит одно целое число `N` (`1\ ≤\ N\ ≤\ 2000`) – количество нот в мелодии. Вторая строка содержит `N` целых чисел 0, 1, 2, 4, 8 и 16 – обозначения длительности нот в мелодии.

Вывести одно число — продолжительность мелодии в секундах с точностью `10^{-3}`.

Пример ввода 1

4
1 1 1 0

Пример вывода 1

10.000

Пример ввода 2

5
1 2 4 8 16

Пример вывода 2

3.875

B. Лесопилка

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Джек владеет лесопилкой. Ему нужно распилить длинное бревно на части одинаковой длины. Перед распиловкой Джек может установить на автоматической пиле длину кусков, на которые будет разделено бревно. Длина кусков выбирается из нескольких возможных настроек. Остаток бревна меньше длины распиловки выбрасывается.

Определите, какая из настроек пилы позволит Джеку минимизировать длину остатка бревна.

Первая строка ввода содержит одно целое число `N` (`2\ ≤\ N\ ≤\ 10`) — количество настроек пилы. Вторая строка содержит `N` целых чисел от 1 до 500 — настройки длины кусков. Третья строка содержит одно целое число `L` (`1\ ≤\ L\ ≤\ 3000`) – длина бревна.

Вывести одно число — длину кусков, на которые нужно распилить бревно, из списка возможных настроек, минимизирующую длину остатка. Если существует несколько вариантов, то можно вывести любой из них.

Пример ввода 1

3
5 6 8
103

Пример вывода 1

Пример ввода 2

4
7 3 5 13
1366

Пример вывода 2

C. Дроиды

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Управление дроидом непростая задача. Еще более сложная задача — управлять несколькими дроидами. В этой задаче вам нужно передвинуть двух дроидов в новые позиции в трехмерном пространстве, избегая их столкновения. Дроиды могут перемещаться только на 1 единицу длины параллельно оси координат `X`, `Y` или `Z`, либо оставаться на месте. Дроиды не могут занимать одну точку в пространстве одновременно или меняться местами за один шаг, если они находились в соседних позициях в пространстве.

Напишите программу, которая выполнит перемещение дроидов без столкновения не более чем за 7000 шагов.

Первая строка ввода содержит шесть целых чисел — начальные координаты дроидов `X_1,\ Y_1,\ Z_1,\ X_2,\ Y_2,\ Z_2`. Вторая строка ввода содержит шесть целых чисел — конечные координаты дроидов `X_1,\ Y_1,\ Z_1,\ X_2,\ Y_2,\ Z_2`. Значения координат находятся в диапазоне от –1000 до 1000. Начальные и конечные координаты дроидов не совпадают.

Вывести координаты дроидов на каждом шаге, включая начальный и конечный момент времени.

Пример ввода 1

0 0 0 1 1 2
2 2 2 0 0 0

Пример вывода 1

0 0 0 1 1 2
1 0 0 0 1 2
2 0 0 0 0 2
2 1 0 0 0 1
2 2 0 0 0 0
2 2 1 0 0 0
2 2 2 0 0 0

Пример ввода 2

0 0 0 1 0 0
1 0 0 0 0 0

Пример вывода 2

0 0 0 1 0 0
0 1 0 0 0 0
1 1 0 0 0 0
1 0 0 0 0 0

D. Магнитики

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Компания распространяет в рекламных целях серию магнитиков на холодильник. Магнитики имеют форму многоугольника и помещаются в конверт прямоугольной формы. Конверт для магнитика должен иметь минимальную ширину, высота конверта несущественна.

Напишите программу, вычисляющую минимальную ширину конверта для магнитика.

Первая строка ввода содержит одно целое число `N` (`3\ ≤\ N\ ≤\ 100`) — количество углов в многоугольнике. Каждая из следующих `N` строк содержит по два целых числа `X_i,\ Y_i` (`-10^5\ ≤\ X_i,\ Y_i\ ≤\ 10^5`) – координаты вершин многоугольника в порядке обходе против часовой стрелки. Многоугольник может быть невыпуклым, имеет ненулевую площадь и в нём нет самопересечений.

Вывести одно число — минимальную ширину конверта для магнитика с точностью `10^-5`.

Пример ввода 1

Пример вывода 1

2.00000

Пример ввода 2

Пример вывода 2

28.81678

E. Снукер

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Снукер — это разновидность бильярдной игры, в которой используются разноцветные шары: несколько красных шаров и по одному шару жёлтого, зелёного, коричневого, синего, розового и чёрного цветов. Игрок забивает шары разных цветов в лузы. Забивание шара в лузу оценивается в определенное количество очков в зависимости от цвета шара: красный (red) шар — 1 очко, жёлтый (yellow) — 2 очка, зелёный (green) — 3 очка, коричневый (brown) — 4 очка, синий (blue) — 5 очков, розовый (pink) — 6 очков, чёрный (black) — 7 очков. Если игрок не может забить шар в лузу по правилам, то ход передается другому игроку или игра заканчивается. После красного шара игрок должен забивать в лузу только шар не красного цвета, а после не красного шара нужно забивать красный шар, если на столе остался хотя бы один красный шар, иначе можно бить по любому шару. При этом, пока красные шары остаются на столе, забитые шары не красного цвета выставляются на свои исходные позиции. Игрок может начинать свой ход с шара любого цвета, но при наличии на столе не красных шаров, выгоднее начинать ход с них.

Напишите программу, вычисляющий максимальное количество очков, которое может получить игрок при своем ходе, если он не сделает ошибок.

Первая строка ввода содержит одно целое число `N` (`1\ ≤\ N\ ≤\ 21`). Далее следует `N` строк, в каждой строке содержится название цвета шара на столе.

Вывести одно целое число — максимальное количество очков, которое может получить игрок для заданного набора шаров на столе.

Пример ввода 1

5
red
black
pink
red
red

Пример вывода 1

Пояснение к примеру: игрок забивает черный шар, который возвращается на стол, затем красный, затем чёрный, затем красный, затем чёрный, затем красный, затем чёрный (красных шаров больше нет — шары на стол не возвращаются) и розовый. Таким образом игрок получает 7+1+7+1+7+1+7+6=37 очков.

Пример ввода 2

3
blue
black
pink

Пример вывода 2

Пример ввода 3

8
yellow
green
brown
red
red
red
red
red

Пример вывода 3

Пример ввода 4

2
red
red

Пример вывода 4

F. Солнечный город

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

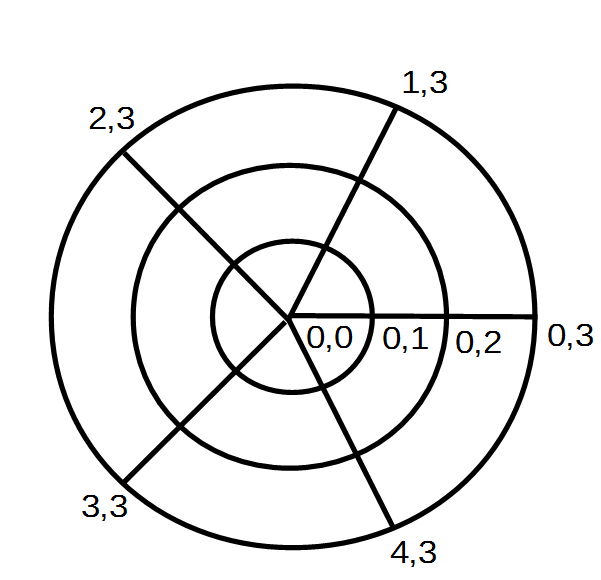
Солнечный город имеет форму круга радиусом `R` и состоит из `N` кольцевых и `M` радиальных улиц. Кольцевые улицы расположены на равном расстоянии `R/N` друг от друга, радиальные делят город на сектора с одинаковым углом. Перекрестки в городе обозначаются номером радиальной улицы (от 0 до `M-1`) и номером кольцевой улицы (от 1 до `N`), центральная площадь города имеет координаты 0,0.

Напишите программу, вычисляющую минимальное расстояние между двумя перекрестками города.

Первая строка ввода содержит три целых числа `M,\ N` (`1\ ≤\ N,\ M\ ≤\ 100`) и `R` (`1\ ≤\ R\ ≤\ 1000`) – количество радиальных и кольцевых улиц и радиус города. Вторая строка ввода содержит четыре целых числа `r_1,\ c_1,\ r_2,\ c_2` (`0\ ≤\ r_1,\ r_2\ ≤\ M-1`, `0\ ≤\ c_1,\ c_2\ ≤\ N`) – координаты двух перекрестков.

Вывести одно число — минимальное расстояние между заданными перекрестками города с точностью `10^{-6}`.

Пример ввода

5 3 2
0 3 1 2

Пример вывода

2.342183

G. Король холма

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

В соревновании "Король холма" один из участников назначается "королём", а остальные участники по очереди бросают ему вызов и победитель становится новым "королём". Проигравший участник больше в соревновании не участвует. Победителем соревнований становится последний "король". Петя участвует в соревновании и хочет узнать, в каком порядке должны происходить схватки, чтобы он стал победителем соревнований.

Первая строка ввода содержит одно целое числа `N` (`1\ ≤\ N\ ≤\ 1000`) — количество участников соревнований. Участники имеют номера с 0 по `N-1`. Петя имеет номер 0. Далее следует `N` строк, содержащих по `N` символов – матрица `A`, показывающая итоги схваток участников. Символ 0 в `i`-й строке и `j`-м столбце матрицы означает, что участник `i` проигрывает схватку против участника `j`; символ 1 — что участник `i` побеждает участника `j`, символ X находится в позиции `i=j`. Гарантируется, что `A_{i,j}=1-A_{j,i}` для `i\ ≠\ j`.

Вывести `N` целых чисел — начального короля и порядок, в котором происходят схватки остальных участников с королём. Если существует несколько вариантов, то можно вывести любой из них. Если ни одного варианта нет, то вывести сообщение "impossible".

Пример ввода 1

3
X10
0X1
10X

Пример вывода 1

1 2 0

Пример ввода 2

3
X10
0X0
11X

Пример вывода 2

impossible

H. Обмен

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Петя получил на обед 1 литр розовой газировки, но он любит синюю газировку. Он может выменять синюю газировку в обмен на розовую у других учеников. Остальные ученики на обеде сидят за длинным столом. Петя может идти вдоль стола только слева направо, меняя один сорт газировки на другой. Каждый ученик любит какой-то сорт газировки и может поменять имеющийся у него в неограниченном количестве сорт газировки на свой любимый сорт по некоторому курсу обмена. Петя хочет получить как можно больше синей газировки.

Первая строка ввода содержит одно целое число `N` (`0\ ≤\ N\ ≤\ 100000`) — количество учеников за столом. Далее следует `N` строк, содержащих по два слова `O` и `W` и одно вещественное число `R` (`0.5\ <\ R\ <\ 2`) – информацию о возможных обменах в порядке слева направо. За `X` литров газировки сорта `W` Петя может получить `R*X` литров газировки сорта `O`. Названия сортов газировки могут иметь от 1 до 10 символов и не содержат пробелов.

В первой строке вывести одно вещественное число – максимальный объем синей газировки, который может получить Петя в экспоненциальной форме: `d."ddddd"`E`p`. Эта запись означает, что ответ равен `d."ddddd"*10^p`, здесь число d.ddddd должно иметь ровно 5 цифр после точки и находиться в диапазоне от 1.00000 до 9.99999. Если ответ равен 0, то вывести 0.00000E0.

Пример ввода 1

3
blue pink 1.0
red pink 1.5
blue red 1.0

Пример вывода 1

1.50000E0

Пример ввода 2

2
blue red 1.0
red pink 1.5

Пример вывода 2

0.00000E0

Пример ввода 3

4
orange pink 1.9
yellow orange 1.9
green yellow 1.9
blue green 1.9

Пример вывода 3

1.30321E1

I. Таблица результатов

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

На соревнования на программированию прибыло слишком много команд, чтобы их можно было показать на мониторе. Поэтому Пете приходится отслеживать успехи своей любимой команды, используя информацию о принятых задачах команд. Команды в рейтинге сортируются в порядке уменьшения успешно сданных задач, а при равенстве количества задач — в порядке увеличения штрафного времени. Если равны и количество задач и время, то команды упорядочиваются по их номеру. Любимая команда Пети имеет номер 1.

Первая строка ввода содержит два целых числа — количество команд `N` (`1\ ≤\ N\ ≤\ 100000`) и количество событий `M` (`1\ ≤\ M\ ≤\ 100000`). Далее следует `M` строк, содержащих по два целых числа – информацию о произошедшем событии: номер команды `t` (`1\ ≤\ t\ ≤\ N`), успешно сдавшей очередную задачу, и добавляемое штрафное время `p` (`1\ ≤\ p\ ≤\ 1000`).

Вывести `M` строк — в `i`-й строке выводится рейтинг команды 1 после `i`-го события.

Пример ввода

Пример вывода

28/10/2017	Очный тур региональных отборочных командных соревнований для школьников (C)
09/07/2018	Лето 2018 - 7 (упрощенное) (E)

28/10/2017	Очный тур региональных отборочных командных соревнований для школьников (F)
02/09/2022	Входной контроль (VP, 3 курс) (проводит sartasova) (F)

28/10/2017	Очный тур региональных отборочных командных соревнований для школьников (G)
05/07/2021	Лето 2021-4 (E)
29/06/2022	Лето 2022-2 (D)

Назад

Подразделы

Другие разделы

Дата и время

Авторизация

Задачи очного тура отборочных командных соревнований школьников

A. Музыкальные стулья

B. Лесопилка

C. Дроиды

D. Магнитики

E. Снукер

F. Солнечный город

G. Король холма

H. Обмен

I. Таблица результатов