Задачи 1 тура регионального олимпиады по информатике 2016

Петр участвует в конкурсе, в котором разыгрывается `n` призов. Призы пронумерованы от 1 до `n`.

По итогам конкурса участник может набрать от 2 до `n` баллов. Если участник наберет `k` баллов, то он получит один из призов с номером от 1 до `k`. Перед тем, как участник выберет свой приз, ведущий конкурса удаляет один из призов из списка. Затем участник может выбрать любой приз из оставшихся `k\ -\ 1`.

Список призов стал известен Петру. Он определил для каждого приза его ценность, для `i`-го приза она задается целым числом `a_i`.

Требуется написать программу, которая по заданным ценностям призов определяет для каждого `k` от 2 до `n`, приз с какой максимальной ценностью гарантированно достанется Петру, если он наберет в конкурсе `k` баллов.

Первая строка входного файла содержит число `n` (`2 ≤ n ≤ 100 000`). Вторая строка этого файла содержит `n` целых чисел: `a_1,\ a_2,\ …,\ a_n` (`1\ ≤\ a_i\ ≤\ 10^9`).

Выходной файл должен содержать одну строку, содержащую `n - 1` целых чисел: для каждого `k` от 2 до `n` должна быть выведена ценность приза, который достанется Петру, если он наберет `k` баллов.

5
1 3 4 2 5

1 3 3 4

Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.

По запросу сообщается результат окончательной проверки на каждом тесте.

Для освоения Марса требуется построить исследовательскую базу. База должна состоять из `n` одинаковых модулей. Каждый модуль представляет собой жилой отсек, который в основании имеет форму прямоугольника размером `a times b` метров.

Для повышения надежности модулей инженеры могут добавить вокруг каждого модуля дополнительный защитный слой. Толщина этого слоя должна составлять целое число метров, и все модули должны иметь одинаковую толщину защитного слоя. Модуль с защитным слоем, толщина которой равна `d` метрам, будет иметь в основании форму прямоугольника размером `(a + 2d) times (b + 2d)` метров.

Все модули должны быть расположены на заранее подготовленном прямоугольном поле размером `w times h` метров. При этом они должны быть организованы в виде регулярной сетки: их стороны должны быть параллельны сторонам поля, и модули должны быть ориентированы одинаково.

Требуется написать программу, которая по заданным количеству и размеру модулей, а также размеру поля для их размещения, определяет максимальную толщину дополнительного защитного слоя, который можно добавить к каждому модулю.

Входной файл содержит пять разделенных пробелами целых чисел: `n`, `a`, `b`, `w` и `h` (`1 ≤ n,\ a,\ b,\ w,\ h ≤ 10^{18}`). Гарантируется, что без дополнительного защитного слоя все модули можно разместить в поселении описанным образом.

Выходной файл должен содержать одно целое число: максимальную возможную толщину дополнительного защитного слоя. Если дополнительный защитный слой установить не удастся, требуется вывести число 0.

11 2 3 21 25

2

1 5 5 6 6

0

Пояснение к примерам

В первом примере можно установить дополнительный защитный слой толщиной 2 метра и разместить модули на поле, как показано на рисунке.

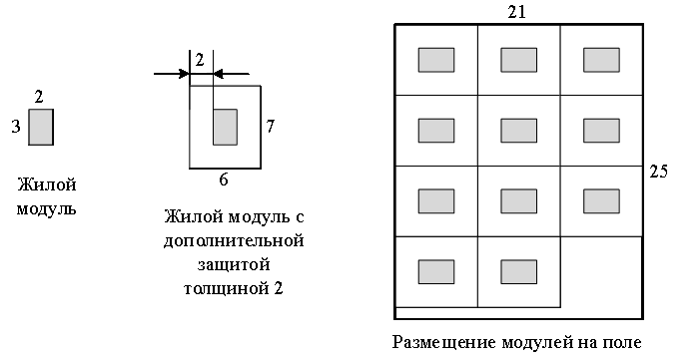
Во втором примере жилой отсек имеет в основании размер `5 times 5` метров, а поле – размер `6 times 6` метров. Добавить дополнительный защитный слой к модулю нельзя.

`1 ≤ n ≤ 1000`, `1 ≤ a,\ b,\ w,\ h ≤ 1000`.

Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.

`1 ≤ n ≤ 1000`, `1 ≤ a,\ b,\ w,\ h\ ≤ 10^9`.

Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.

`1 ≤ n ≤ 10^9`, `1 ≤ a,\ b,\ w,\ h\ ≤ 10^{18}`.

В этой подзадаче 8 тестов, каждый тест оценивается в 3 балла. Баллы за каждый тест начисляются независимо.

`1 ≤ n ≤ 10^{18}`, `1 ≤ a,\ b,\ w,\ h\ ≤ 10^{18}`.

В этой подзадаче 9 тестов, каждый тест оценивается в 3 балла. Баллы за каждый тест начисляются независимо.

По запросу сообщается результат окончательной проверки на каждом тесте.

Рассмотрим строку `s`, состоящую из строчных букв латинского алфавита. Примером такой строки является, например, строка «abba».

Подстрокой строки s называется строка, составленная из одного или нескольких подряд идущих символов строки `s`. Обозначим как `W(s)` множество, состоящее из всех возможных подстрок строки s. При этом каждая подстрока входит в это множество не более одного раза, даже если она встречается в строке `s` несколько раз.

Например, `W(tt{«"abba"»})\ =\ {tt{«a»},\ tt{«b»},\ tt{«"ab"»},\ tt{«"ba"»},\ tt{«b""b»},\ tt{«"abb"»},\ tt{«"bba"»},\ tt{«"abba"»}\ }`.

Подпоследовательностью строки `s` называется строка, которую можно получить из `s` удалением произвольного числа символов. Обозначим как `Y(s)` множество, состоящее из всех возможных подпоследовательностей строки `s`. Аналогично `W(s)`, каждая подпоследовательность строки `s` включается в `Y(s)` ровно один раз, даже если она может быть получена несколькими способами удаления символов из строки `s`. Поскольку любая подстрока строки `s` является также ее подпоследовательностью, то множество `Y(s)` включает в себя `W(s)`, но может содержать также и другие строки.

Например, `Y(tt{«"abba"»}) = W(tt{«"abba"»}) uu {tt{«"aa"»},\ tt{«"aba"»}\ }`. Знак `uu` обозначает объединение множеств.

Будем называть строку `s` странной, если для нее `W(s)` = `Y(s)`. Так, строка «abba» не является странной, а, например, строка «abb» является, так как для нее `W(tt{«"abb"»})\ =\ Y(tt{«"abb"»})\ =\ {tt{«a»},\ tt{«b»},\ tt{«"ab"»},\ tt{«b""b»},\ tt{«"abb"»}\ }`.

Будем называть странностью строки число ее различных странных подстрок. При вычислении странности подстрока считается один раз, даже если она встречается в строке `s` в качестве подстроки несколько раз. Так, для строки «abba» ее странность равна 7, любая ее подстрока, кроме всей строки, является странной.

Требуется написать программу, которая по заданной строке `s` определяет ее странность.

Входной файл содержит строку `s`, состоящую из строчных букв латинского алфавита. Строка имеет длину от 1 до `200 000`.

Выходной файл должен содержать одно целое число: странность заданной во входном файле строки.

abba

7

В этой задаче четыре подзадачи. Баллы за каждую подзадачу начисляются только в случае, если все тесты для данной подзадачи успешно пройдены.

Строка `s` состоит только из букв «a» и «b». Длина строки `s` не превышает 50.

Длина строки `s` не превышает 50.

Длина строки `s` не превышает 1000.

Длина строки `s` не превышает `200 000`.

По запросу сообщается результат окончательной проверки на каждом тесте.

Железная дорога Флатландии представляет собой прямую, вдоль которой расположены `n` станций. Будем называть участок железной дороги от некоторой станции до следующей перегоном.

Поезд следует от станции 1 до станции `n`, делая остановку на каждой станции. В поезде `k` мест, пронумерованных от 1 до `k`. На поезд продаются билеты, каждый билет характеризуется тремя числами: `s`, `t` и `a`. Такой билет позволяет проехать от станции `s` до станции `t` на месте `a`.

Иван планирует в один из дней летних каникул проехать на поезде от одной станции до другой. Он выяснил, что на поезд в этот день уже продано `m` билетов, и возможно уже нет мест, свободных на всех перегонах между интересующими его станциями. Билет от одной станции до другой на определенное место можно купить, только если это место свободно на всех перегонах между этими станциями.

Иван сообразил, что иногда все равно можно проехать от одной станции до другой, купив несколько билетов и пересаживаясь с одного места на другое на некоторых промежуточных станциях. Разумеется, пересаживаться с места на место неудобно, поэтому Иван хочет купить минимальное количество билетов, чтобы на каждом перегоне у него было свое место.

Иван еще не решил, от какой станции и до какой он поедет. Он записал `q` вариантов поездки, и для каждого из них хочет узнать, какое минимальное число билетов ему придется купить, если он выберет этот вариант.

Требуется написать программу, которая по заданному описанию уже проданных билетов и вариантов поездки Ивана определяет для каждого варианта, какое минимальное количество билетов необходимо купить, чтобы совершить такую поездку.

Первая строка входного файла содержит числа `n`, `m` и `k` (`2 ≤ n ≤ 200 000`, `0 ≤ m ≤ 200 000`, `1 ≤ k ≤ 200 000`) – количество станций, количество уже проданных билетов и количество мест в поезде. Последующие `m` строк содержат информацию о проданных билетах. Каждая строка содержит три числа: `s_i`, `t_i` и `a_i` – номер станции, от которой куплен билет, номер станции, до которой куплен билет, и номер места, на которое куплен билет (`1 ≤ s_i < t_i ≤ n`, `1 ≤ a_i ≤ k`). Гарантируется, что все билеты куплены таким образом, что ни на каком перегоне ни на какое место нет более одного билета.

Далее идет строка, которая содержит число `q` (`1 ≤ q ≤ 200 000`). Последующие `q` строк содержат описания вариантов поездки. Каждая строка содержат два числа: `f_j`, `d_j` – номер станции, от которой Иван хочет поехать в этом варианте, и номер станции, до которой он хочет поехать (`1 ≤ f_j < d_j ≤ n`).

Выходной файл должен содержать `q` чисел: для каждого варианта поездки требуется вывести минимальное количество билетов, которое необходимо купить Ивану, чтобы совершить соответствующую поездку. Если поездку совершить невозможно, то для этого варианта требуется вывести `-1`.

5 4 3
1 4 1
2 5 3
2 3 2
4 5 2
3
1 5
3 5
4 5

-1
2
1

На перегоне от 2-й до 3-й станции все места заняты, поэтому проехать от 1-й до 5-й станции невозможно. От 3-й до 5-й станции можно проехать, используя два билета: от 3-й до 4-й станции на место 2 и от 4-й до 5-й на место 1. От 4-й до 5-й станции можно проехать, используя один билет на место 1.

В этой задаче три подзадачи. Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.

Внимание! Тест из примера не подходит под ограничения для подзадач 1 и 2, но решение принимается на проверку только в том случае, если оно выводит правильный ответ на тесте из примера. Решение должно выводить правильный ответ на тест даже, если оно рассчитано на решение только каких-либо из подзадач 1 и 2.

`n ≤ 100`, `m ≤ 100`, `k ≤ 100`, `q\ =\ 1`

`n ≤ 200 000`, `m ≤ 200 000`, `k ≤ 200 000`, `q\ =\ 1`

`n ≤ 200 000`, `m ≤ 200 000`, `k ≤ 200 000`, `q\ ≤\ 200 000`

По запросу сообщаются баллы за каждую подзадачу.