Подразделы
Другие разделы
Дата и время
10/03/2026 14:31:05
 Разбор задач отборочных командных соревнований школьников 2013
Разбор задач отборочных командных соревнований школьников 2013
 Разбор задачи A. Абак
Разбор задачи A. Абак
Тема: системы счисленияСложность: простая
В задаче рассматривается некоторая система счисления, основанная на десятичной. Стоимость косточки в "небесном" отделении равна `5*10^{(N-i)}`, а в "земном" – `1*10^{(N-i)}`, где `i` – номер проволоки.
Для решения задачи можно воспользоваться стандартным алгоритмом, обеспечивающим преобразование числа в некоторой системе счисления во внутреннее представление.
число:=0 for i:=1 to колво_цифр_в_числе число:=число*основание+цифра[i]
Для ввода и преобразования количества косточек в каждом отделении в число можно написать следующую функцию:
function load(n:integer):int64;
var num:int64;
i,c:integer;
begin
num:=0;
for i:=1 to n do
begin
read(c);
num:=num*10+c;
end;
load:=num;
end;
Так как результат вычислений может превышать `10^15`, то для вычислений нужно использовать тип int64. Основная программа выглядит следующим образом:
var r1,r2:int64; n:integer; begin readln(n); r1:=load(n); // небесное отделение r2:=load(n); // земное отделение writeln(r1*5+r2); end.
 Разбор задачи B. Треугольник Паскаля
Разбор задачи B. Треугольник Паскаля
Тема: реализация программы по заданному алгоритмуСложность: простая
Для нахождения 8 младших разрядов числа нужно все вычисления производить по модулю `10^8`. Если добавить в каждую строку 0-й элемент равный 0, то можно в цикле вычислений не делать проверок на отсутствие элементов в предыдущей строке. В результате программа выглядит следующим образом:
var t:array[1..1000,0..1000]of integer;
n,m,i,j:integer;
begin
read(n,m);
t[1,1]:=1;
for i:=2 to n do
for j:=1 to i do
t[i,j]:=(t[i-1,j-1]+t[i-1,j])mod 100000000;
writeln(t[n,m]);
end.
 Разбор задачи C. Аналитическая машина
Разбор задачи C. Аналитическая машина
Тема: двоичный поиск, генерация программыСложность: высокая
Идея задачи взята из журнала Квант №12 за 1992 год, задача M1347.
Пусть у нас есть две последовательности из `L+1` и `L` чисел и нужно найти
`(L+1)`-е по возрастанию число.
Расположим эти последовательности в ряд друг под другом, первую
в порядке возрастания, вторую в порядке убывания, как показано ниже,
и соединим соседние числа стрелками, направленными от большего числа
к меньшему.
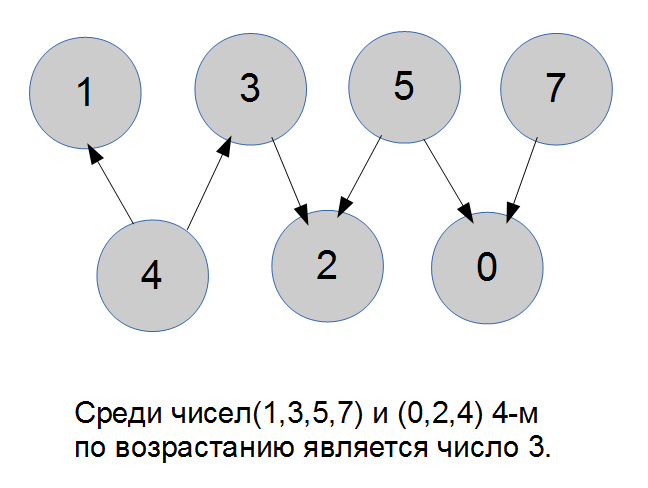
Если какая стрелка направлена вниз, то справа от нее все стрелки
тоже будут направлены вниз, аналогично, если какая-то стрелка направлена
вверх, то слева от нее все стрелки направлены вверх. Также в этой схеме
количество меньших чисел в другом ряду плюс количество меньших
чисел в своем ряду равно `L`. Если у какого-то числа стрелка справа
направлена вниз, а слева – вверх, то это искомое `(L+1)`-е по возрастанию число.
Для нахождения соседних стрелок, направленных в разные стороны, среди `2*L`
стрелок достаточно `log_2(2*L)` сравнений (более подробное объяснение приводится в журнале).
Если среди элементов последовательностей длиной `N` и `M` выделить кандидатов
на `K`-й элемент, то их будет либо `L+1` из одной последовательности
и `L` из другой и среди этих чисел искомый `K`-й элемент будет `(L+1)`-м
(рассмотренная задача), либо `L` из одной и `L` из другой и `K`-й будет `L`-м или
`(L+1)`-м среди выделенных (в этом случае для сведения задачи к предыдущей нужно добавить
один фиктивный элемент, так чтобы нужно было искать `(L+1)`-й элемент).
Время работы и длина программы `O(N+M)`.
 Разбор задачи D. Прятки
Разбор задачи D. Прятки
Тема: моделированиеСложность: средняя
Так как ограничения по координатам небольшие, можно промоделировать расстановку ящиков и выявить клетки, являющиеся видимыми с 4 сторон. Время работы программы равно O(`10^6`). Основания ящиков не пересекаются, поэтому при расстановке ящиков потребуется покрасить не более `10^6` клеток. На каждом из последующих 4 шагов по установлению видимых клеток с каждой стороны двора будут помечены также не более `10^6` клеток. И на последнем шаге нужно выполнить полный перебор с целью подсчета количества непомеченных (невидимых) клеток.
{ обмен местами значений координат,если первая координата больше второй }
procedure swap(var a,b:integer);
var t:integer;
begin
if a>b then
begin
t:=a;
a:=b;
b:=t;
end;
end;
var court:array[1..1000,1..1000]of integer;
i,j,k,n,x1,y1,x2,y2:integer;
begin
read(n);
{ 1 шаг - покраска части двора под ящиками
for k:=1 to n do
begin
read(x1,y1,x2,y2);
swap(x1,x2);
swap(y1,y2);
for i:=y1 to y2-1 do
for j:=x1 to x2-1 do
court[i,j]:=2;
end;
{ 2 шаг - пометить клетки, видимые с западной стороны }
for i:=1 to 1000 do
for j:=1 to 1000 do
if court[i,j]=2 then break
else court[i,j]=1;
{ 3,4,5 шаг - аналогично, с изменением направления прохождения циклов }
{ ... }
{ 6 шаг - подсчет количества невидимых клеток }
k:=0;
for i:=1 to 1000 do
for j:=1 to 1000 do
if court[i,j]=0 then k:=k+1;
writeln(k);
end.
 Разбор задачи F. Микропрограммирование
Разбор задачи F. Микропрограммирование
Тема: динамическое программированиеСложность: средняя
Пусть первоначально в регистре находится число `x>0`. При выполнении вычислений значение в регистре не может стать меньше значения на вершине стека, так как значение в регистре изменяется только при сложении. Из этих же соображений нельзя получить число, не являющееся кратным числа `x`. По завершении вычислений стек должен быть пустым.
Операции ^ и + являются скобками, каждой операции ^ в минимальной программе должна быть соответствующая операция + и наоборот. Найдем операцию ^, соответствующую последней операции +. В части программы до ^ (возможно пустой) вычисляется значение `a*x`, которое сохраняется в стеке, затем выполняется некоторая последовательность действий, приводящее к получению в регистре `k*a*x` (число, являющееся кратным числа `a*x`) и затем происходит сложение.
`a*x+k*a*x\ =\ N*x`
`a+k*a\ =\ N`
`a*(k+1)\ =\ N`
Таким образом для получения оптимальной программы нужно проанализировать все возможные разложения числа `N` на множители, включая `a=1`, и для каждого множителя найти наиболее короткую программу. Чтобы не находить для какого-то значения минимальную программу несколько раз, нужно запоминать вычисленный результат в массиве. Итоговая программа выглядит так:
uses math;
procedure minlen(var r:string; const s:string);
begin
if length(r)>length(s) then { новый вариант короче? }
r:=s; { заменяем на него }
end;
var prog:array[1..1000] of string;
function optprog(n:integer):string;
var a:integer;
begin
if (n>1) and (prog[n]='') then { ранее не вычислялось }
begin
prog[n]:='^'+optprog(n-1)+'+'; { для случая a=1 }
for a:=2 to trunc(sqrt(n)) do
if n mod a=0 then { a является множителем n }
begin { n div a - второй множитель, (k+1) в формуле }
minlen(prog[n],optprog(a)+'^'+optprog(n div a-1)+'+');
{ переставляем множители местами }
minlen(prog[n],optprog(n div a)+'^'+optprog(a-1)+'+');
end;
end;
optprog:=prog[n];
end;
var n:integer;
begin
read(n);
writeln(optprog(n));
end.
 Разбор задачи I. Забор
Разбор задачи I. Забор
Тема: динамическое программированиеСложность: высокая
Фигура с наименьшим периметром должна быть выпуклой и
лежать внутри некоторого прямоугольника площадью `H*W≥S` с
минимальным периметром `P=2*(H+W)`.
Перебираем все варианты размещения таких прямоугольников
и в каждом местоположении запускаем динамику с параметрами (верхняя граница,
нижняя граница, направление движения границ для обеспечения выпуклости,
оставшаяся неиспользованная площадь `H*W-S`) и считаем количество покрытых отмеченных клеток.
Если найдено лучшее решения по покрытию для неиспользованной площади равной `H*W-S`, запоминаем это решение.
После перебора лучшее решение выводим.
Время работы `O(N^3*M^3)`.

 Начало
Начало Соревнования
Соревнования