Назад
 Начало Начало |
 Соревнования Соревнования |
| 2013 |
Подразделы
Другие разделы
| Задачи Южно-Уральского командного чемпионата 2013 |
| Задачи отборочных командных соревнований школьников 2013 |
| Задачи муниципального этапа олимпиады школьников по информатике 2013 |
Дата и время
17/02/2026 20:05:52
 Задачи заочного тура личного первенства 2013
Задачи заочного тура личного первенства 2013
 A. Мультипликативный цифровой корень
A. Мультипликативный цифровой корень
 Реализация заданного алгоритма
Реализация заданного алгоритмаОлимпиадные задачи на русском языке

| 05/09/2013 | Заочный тур личного первенства (A) |
Ограничения: время – 200ms/500ms, память – 128MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Произведение цифр многоразрядного числа всегда меньше самого числа. Если эту операцию применить
несколько раз, то в конце концов мы получим число из одной цифры. Это число называют мультипликативным цифровым корнем числа, а количество
шагов до получения числа из одной цифры – мультипликативной стойкостью числа. Например, для числа 77 потребуется 4 шага:
77 — 49 — 36 — 18 — 8.
Напишите программу, которая вычисляет мультипликативную стойкость и цифровой корень заданного числа.
Первая строка ввода содержит одно целое число `N` (`0\ ≤\ N\ ≤\ 10^18`).
Вывести два целых числа, разделенных пробелом, – мультипликативную стойкость и мультипликативный цифровой корень числа `N`.
Пример ввода 1
77
Пример вывода 1
4 8
Пример ввода 2
1
Пример вывода 2
0 1
 B. Угадайка
B. Угадайка
 Простые числа, разложение на множители
Простые числа, разложение на множителиОлимпиадные задачи на русском языке

| 05/09/2013 | Заочный тур личного первенства (B) |
Ограничения: время – 1s/2s, память – 128MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Напишите программу, которая может выиграть в следующую игру. Некто задумал число от 2 до 1000.
Вы называете пробные числа `k_i` в диапазоне от 2 до `10^6`. Если задуманное число делится на `k_i` без остатка, то задуманное число заменяется на частное от деления,
иначе к задуманному числу прибавляется пробное число `k_i`, и игра продолжается. После каждого хода вы получаете информацию, было выполнено деление или добавление пробного числа к задуманному числу. Если после изменения число
становится равным 1, вы выигрываете. Если вы не сможете получить 1 после 1000 ходов, то вы проигрываете.
Называть числа, уже названные ранее, запрещается.
Вы должны написать подпрограмму с именем solve без параметров.
void solve(); // С/С++ procedure solve; // Pascal
Для выполнения хода ваша подпрограмма должна вызывать подпрограмму check с пробным числом в качестве аргумента. Эта функция возвращает 1 (true), если было выполнено деление, или 0 (false), если было выполнено сложение. Если срабатывает условие завершения (получение 1 или количество ходов стало больше 1000), то функция завершает выполнение программы.
int check(int k); // С/С++ function check(k:integer):boolean; // Pascal
Пересылаемое на проверку решение должно содержать только подпрограмму solve, вспомогательные функции,
команды #include (в C/C++) и глобальные переменные. В подпрограммах не должен выполняться ввод или вывод.
Пример программы на языке C/C++:
void solve()
{ for(int i=2;i<=1000;++i)
check(i);
}
Пример программы на языке Pascal:
procedure solve;
var i:integer;
begin
for i:=2 to 1000 do
check(i);
end;
 C. Обклейка кубика
C. Обклейка кубика
 Не классифицирована
Не классифицирована
| 05/09/2013 | Заочный тур личного первенства (C) |
Ограничения: время – 200ms/500ms, память – 128MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Из костяшек домино легко можно составить одномерную цепочку,
в которой соприкасающиеся квадраты соседних костяшек имеют одинаковое количество точек.
В книге М.Гардера "Математические досуги" описывается двух- и трехмерное домино,
придуманное Британским специалистом по комбинаторному анализу, преподавателем Королевской военной академии Александром Макмагоном.
Если разделить квадраты двумя диагоналями на четыре части и раскрасить их всеми возможными способами в три цвета, то 24 различных разноцветных
квадрата. Из них можно сложить прямоугольник 4x6 таким образом, что каждая пара соприкающихся сторон квадратов имеют одинаковый цвет.
При этом можно сделать так, чтобы край прямоугольника был одного цвета. На рисунке показано одно из таких решений.
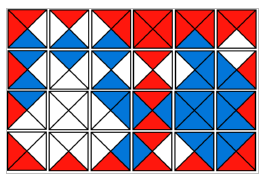
С помощью компьютера было подчитано, что количество способов составить такой прямоугольник с краем одного цвета равно
12261 (решения, получаемые одно из другого поворотами и отражениями, считаются одинаковыми).
Поверхность куба 2х2х2 тоже содержит 24 единичных квадрата, и его поверхность можно оклеить квадратами Макмагона. На рисунке показано одно из таких решений.

Ваша задача – подсчитать количество способов оклеить куб 2х2х2 квадратами Макмагона. Решения, получаемые одно из другого поворотами и отражениями, считаются одинаковыми.
В качестве ответа вы должны переслать файл, содержащий только одно число – количество способов (в качестве языка программирования указать Pascal или C).
Оценка решений этой задачи будет проводиться после
завершения соревнований. 100 баллов получит правильное решение. Ошибка в ответе на 4 порядка или более – 0 баллов.
Промежуточные решения получают оценку `100-25*|log_10\ R\ -\ log_10\ N|`, где `N` – правильный ответ, `R` – ваш ответ.
Автор головоломки: Авилов Н.И.

