Начало
Соревнования
Задачи 2 тура областной олимпиады по информатике 2013
5. Игральные кубики
Вывод формулыОлимпиадные задачи на русском языке
| 21/01/2013 | Областная олимпиада школьников по информатике. II тур. (5) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Юный математик Матвей интересуется теорией вероятностей, и по этой причине у него
всегда есть с собой несколько стандартных шестигранных игральных кубиков. Стандартный шестигранный
кубик имеет три противолежащих пары граней, которые размечены таким образом, что напротив грани с числом 1
находится грань с числом 6, напротив грани с числом 2 — грань с числом 5 и напротив грани с
числом 3 — грань с числом 4.
Анализируя различные игры с шестигранными кубиками, Матвей придумал новую игру. В эту игру играют
два игрока, и проходит она следующим образом: первый игрок бросает один или
несколько стандартных кубиков (количество кубиков он определяет сам). После этого первому игроку
начисляется количество очков, равное сумме чисел, оказавшихся на верхних гранях всех кубиков, а второму
игроку — сумма чисел, оказавшихся на нижних гранях этих кубиков. Побеждает тот, кто набрал больше очков.
Например, если был брошен один кубик, и на верхней его грани выпало число два, то первый игрок
получает два очка, а второй — пять. В свою очередь, если было брошено два кубика и на их верхних
гранях выпало по единице, то первый игрок получает также два очка, а второй игрок – двенадцать очков, так
как на нижних гранях этих кубиков оказались шестерки.
Матвей рассказал об этой игре своему другу, юному информатику Фоме, и они начали играть в неё через
Интернет. Поскольку Фома не видит результат броска и не знает, сколько кубиков бросает
Матвей как первый игрок, то о набранных каждым игроком очках он узнает только от Матвея. Чтобы
проверить достоверность этой информации, Фома решил узнать, какое минимальное и максимальное количество
очков мог получить он, как второй игрок, если известно, сколько очков набрал Матвей.
Требуется написать программу, которая по количеству очков, набранных первым игроком после броска, определяет
наименьшее и наибольшее количество очков, которые может получить второй игрок за этот бросок.
Формат входного файла
Первая строка входного файла содержит одно целое положительное число `n` — количество очков, которые получил
первый игрок (`1\ ≤\ n\ ≤\ 10^10`).
Формат выходного файла
Выходной файл должен содержать два разделенных пробелом целых числа: минимальное и максимальное количество
очков соответственно, которые мог набрать второй игрок при таком броске кубиков.
Пример ввода 1
2
Пример вывода 1
5 12
Пример ввода 2
36
Пример вывода 2
6 216
Система оценивания
Правильные решения для тестов, в которых `1\ ≤\ n\ ≤\ 1000`, будут оцениваться из 50 баллов.
Источник: региональный этап Всероссийской олимпиады по информатике 2012/2013, http://neerc.ifmo.ru/school/ 6. Имена
Жадные алгоритмыОлимпиадные задачи на русском языке
| 21/01/2013 | Областная олимпиада школьников по информатике. II тур. (6) |
| 10/07/2017 | Лето 2017 - 8 (C) |
| 07/07/2023 | Лето 2023-6 сложные (командное) (I) |
| 05/07/2024 | Лето 2024-6 сложные (командное) (I) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
На далекой планете Тау Кита есть непонятные нам обычаи. Например, таукитяне очень необычно для землян
выбирают имена своим детям. Родители так выбирают имя ребенку, чтобы оно могло быть получено как удалением
некоторого набора букв из имени отца, так и удалением некоторого набора букв из имени матери. Например, если
отца зовут "abacaba", а мать — "bbccaa", то их ребенок может носить имена "a", "bba", "bcaa", но не может носить
имена "aaa", "ab" или "bbc". Возможно, что имя ребенка совпадает с именем отца и/или матери, если оно может быть
получено из имени другого родителя удалением нескольких (возможно, ни одной) букв.
Пусть отец по имени `X` и мать по имени `Y` выбирают имя своему новорожденному ребенку. Так как в таукитянских
школах учеников часто вызывают к доске в лексикографическом порядке имен учеников, то есть в порядке
следования имен в словаре, то они хотят выбрать своему ребенку такое имя, чтобы оно лексикографически
следовало как можно позже.
Формально, строка `S` лексикографически больше строки `T`, если выполняется одно из двух условий:
- строка `T` получается из `S` удалением одной или более букв с конца строки `S`;
- первые `(i-1)` символов строк `T` и `S` не различаются, а буква в `i`-й позиции строки `T` следует в алфавите раньше буквы в `i`-й позиции строки `S`.
Требуется написать программу, которая по именам отца и матери находит лексикографически наибольшее имя для их ребенка.
Формат входного файла
Первая строка входного файла содержит имя отца `X`. Вторая строка входного файла содержит имя матери `Y`. Каждое имя
состоит из строчных букв латинского алфавита, включает хотя бы одну букву и имеет длину не более `10^5` букв.
Формат выходного файла
Выходной файл должен содержать искомое лексикографически наибольшее из возможных имен ребенка. В случае, если
подходящего имени для ребенка не существует, выходной файл должен быть пустым (или его единственная строка должна быть пустой).
Пример ввода 1
abcabca abcda
Пример вывода 1
ca
Пример ввода 2
ccba accbbaa
Пример вывода 2
ccba
Пояснения к примеру
В первом примере имя ребенка не может начинаться с буквы большей с, так как имя отца не содержит таких
букв. Буква с содержится в обоих именах, следовательно, имя ребенка может начинаться с этой буквы.
Единственная буква, которая может идти следом за буквой с в имени ребенка — это буква a.
Система оценивания
Правильные решения для тестов, в которых имена содержат только буквы a и b и имеют длину не
более 1000, будут оцениваться из 20 баллов.
Правильные решения для тестов, в которых имена содержат только буквы a и b и имеют длину не
более `10^5`, будут оцениваться из 40 баллов.
Правильные решения для тестов, в которых имена имеют длину не более 1000, будут оцениваться из 40 баллов.
Несмотря на выделение отдельных групп тестов, на окончательную проверку будут приниматься только решения, правильно работающие для всех тестов, приведенных в условии задачи.
Источник: региональный этап Всероссийской олимпиады по информатике 2012/2013, http://neerc.ifmo.ru/school/ 7. Две окружности
Вычислительная геометрияГенерация всех подмножеств, сочетаний, перестановок
Олимпиадные задачи на русском языке
| 21/01/2013 | Областная олимпиада школьников по информатике. II тур. (7) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
Юный футболист Митя обнаружил на школьном футбольном поле две различные окружности, нарисованные едва
заметной белой краской. Вспомнив истории о загадочных кругах на полях, он отметил эти окружности с помощью
небольших камушков. Митя разложил на поле `n` камушков так, чтобы каждый из них находился на одной из окружностей
или даже на их пересечении, если эти окружности пересекаются. Получилось так, что на каждой окружности
размещался хотя бы один камушек. Обладая отличным глазомером, Митя расположил камушки на окружностях
абсолютно точно, без какой-либо погрешности.
На следующий день пошел дождь, краска стерлась, и нарисованные окружности исчезли, но все камушки остались
на своих местах. Теперь Мите очень нужно найти доказательство необычного явления, свидетелем
которого он был, то есть, восстановить окружности.
Требуется написать программу, которая по координатам камушков на поле находит вариант
размещения их на двух несовпадающих окружностях.
Формат входного файла
Первая строка входного файла содержит целое число `n` — количество размещенных Митей камушков
на поле (`2\ ≤\ n\ ≤\ 2000`). Последующие `n` строк содержат целочисленные координаты
камушков `(x_i,\ y_i)` — в каждой строке по одной паре координат, разделенных пробелом (`-10^6\ ≤\ x_i,\ y_i\ ≤\ 10^6`).
Никакие два камушка не размещаются в одной точке. Гарантируется, что ответ для заданного набора камушков существует.
Формат выходного файла
Выходной файл должен содержать две строки. Первая строка должна содержать
последовательность номеров всех камушков, которые принадлежат первой окружности,
вторая строка — последовательность номеров всех камушков, которые принадлежат
второй окружности. Считается, что камушки пронумерованы от 1 до `n` в порядке их
следования во входных данных.
Каждый камушек должен встречаться хотя бы в одной из двух последовательностей.
Если камушек встречается в обеих последовательностях, то это обозначает, что он находится на пересечении окружностей.
Нумерация окружностей не имеет значения, то есть выводить две
последовательности можно в любом порядке. Числа в последовательностях
можно также выводить в произвольном порядке. Каждая
из последовательностей должна содержать не менее одного числа.
Все числа в строках должны быть разделены пробелами.
Если вариантов расположения окружностей несколько, можно выбрать любой из них.
Пример ввода 1
7 1 -1 0 0 1 1 3 1 3 -1 2 0 4 0
Пример вывода 1
6 1 2 3 4 7 5 6
Пример ввода 2
5 -1000000 0 0 1000000 1000000 0 0 -1000000 0 0
Пример вывода 2
1 2 3 4 1 5
Пояснения к примерам
В первом примере одна из искомых окружностей имеет центр в точке с координатами `(1,\ 0)`, а вторая — в точке с координатами `(3,\ 0)`.
Обе окружности имеют радиус равный 1.
Во втором примере центр первой окружности совпадает с началом координат, а радиус равен `10^6`. Вторая
окружность — любая, проходящая через точки `(-10^6,\ 0)` и `(0,\ 0)`.
В обоих примерах возможны и другие правильные ответы.
Система оценивания
Правильные решения для тестов, в которых `2\ ≤\ n\ ≤\ 50`, будут оцениваться из 50 баллов.
Источник: региональный этап Всероссийской олимпиады по информатике 2012/2013, http://neerc.ifmo.ru/school/ 8. Столицы
Динамическое программирование и запоминающие функцииДругие задачи на графы
Олимпиадные задачи на русском языке
| 21/01/2013 | Областная олимпиада школьников по информатике. II тур. (8) |
Ограничения: время – 2s/4s, память – 512MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
В стране Триландии близятся выборы новых столиц. Столицы в Триландии необычные, поскольку ими являются
одновременно сразу три различных города. Такая идея размещения столиц основана на исследованиях эффективности
управления страной, выполненных ведущими экономистами Триландии.
Всего в Триландии `n` городов, из которых некоторые пары городов соединены дорогами и по каждой из них
можно проехать в обе стороны. Время проезда по каждой дороге в
одну сторону равно одному часу. При этом все города соединены дорогами таким образом, что из
каждого города можно добраться в любой другой, причем это можно сделать
единственным способом, если по каждой дороге проезжать не более одного раза и только в одну сторону.
Как показали результаты проведенных триландскими экономистами исследований, управление
страной будет наиболее эффективным, если три столицы будут выбраны так, что время
проезда по кратчайшему пути между каждой парой столиц составит ровно `d` часов. Перед проведением выборов
необходимо знать, сколько существует различных троек городов, удовлетворяющих описанным выше свойствам.
Две тройки городов считаются различными, если в первой тройке есть хотя бы один город,
которого нет во второй тройке, и наоборот.
Требуется написать программу, которая по количеству городов в Триландии и описанию
дорог находит количество троек городов, которые могут быть столицами.
Формат входного файла
Первая строка входного файла содержит два разделенных пробелом целых числа: количество городов в Триландии `n` и
требуемое время в пути между столицами `d` (`3\ ≤\ n\ ≤\ 10^5`, `1\ ≤\ d\ <\ n`). Каждая из последующих `(n–1)` строк
содержит описание одной дороги: пару разделенных пробелом различных целых чисел `a_i` и `b_i` — номера городов,
которые соединены двусторонней дорогой (`1\ ≤\ a_i\ ≤\ n`, `1\ ≤\ b_i\ ≤\ n`, `a_i\ ≠\ b_i`). Каждая пара городов
соединена не более чем одной дорогой.
Формат выходного файла
Выходной файл должен содержать одно целое число — количество подходящих троек городов, которые могут
быть выбраны столицами. В случае, если подходящих троек городов не окажется, выходной файл должен содержать ноль.
Пример ввода 1
4 2 1 2 1 3 1 4
Пример вывода 1
1
Пример ввода 2
7 2 1 2 1 3 1 4 5 1 5 6 5 7
Пример вывода 2
5
Пояснения к примерам
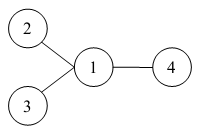
В первом примере существует единственный способ выбрать три столицы: города с номерами 2, 3 и 4. Рисунок, соответствующий первому примеру, приведен ниже.
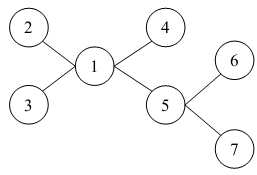
Во втором примере существует четыре варианта выбора трёх столиц из четверки городов: 2, 3, 4 и 5. Можно также выбрать столицами города с номерами 1, 6 и 7. Рисунок, соответствующий второму примеру, приведен ниже.
Система оценивания
Правильные решения для тестов, в которых `3\ ≤\ n\ ≤\ 50`, будут оцениваться из 20 баллов.
Правильные решения для тестов, в которых `3\ ≤\ n\ ≤\ 500`, будут оцениваться из 40 баллов.
Правильные решения для тестов, в которых `3\ ≤\ n\ ≤\ 5000`, будут оцениваться из 60 баллов.
Источник: региональный этап Всероссийской олимпиады по информатике 2012/2013, http://neerc.ifmo.ru/school/ 