Начало
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
Задачи
953. Movies
Динамическое программирование и запоминающие функцииПоиск в глубину (DFS)
Олимпиадные задачи на английском языке
| 03/07/2008 | Лето 2008 дорешивание ( 3K) |
| 07/07/2008 | Лето 2008 - 3 (K) |
Ограничения: время – 1s/2s, память – 128MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
A favorite pastime for big families in Acmestan is going to the movies. It is quite common to see a number of these multi-generation families going together
to watch a movie. Movie theaters in Acmestan have two types of tickets: a single ticket is for exactly one person while
a family ticket allows a parent and their children to enter the theater. Needless to say, a family ticket is always priced
higher than a single ticket, sometimes as high as five times the price of a single ticket.
It is quite challenging for families to decide which ticket arrangement is most economical to buy.
For example, the family depicted in the figure on has four ticket arrangements to choose from:
- Seven single tickets;
- Two family tickets;
- One family ticket (for 0, 1, 2) plus four single tickets for the rest;
- Or, one family ticket (for 1 and his four children) plus single tickets for the remaining two.
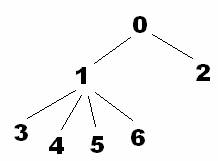
Write a program to determine which ticket arrangement has the least price.
Input
The first line of the input includes two positive integers (`S` and `F`) where `S` is the price of a single ticket and `F` is the price of a
family ticket. The remaining lines of the test case are either the name of a person going by him/herself, or of the form:
`N_1\ N_2\ N_3\ …\ N_k`
where `N_1` is the ID of a parent, with `N_2\ …\ \ N_k` being his/her children. ID's are non-negative integers less then 100,000. No parent will be taking more than 1000 of their children to the movies 
. ID's unique, the ID of a particular person will appear at most twice: once as a parent, and once as a child. There will be at least one person and at most 100,000 people.
. ID's unique, the ID of a particular person will appear at most twice: once as a parent, and once as a child. There will be at least one person and at most 100,000 people. Output
Write the minimal total cost of tickets.
Sample Input 1
1 3 0 1 2 1 3 4 5 6
Sample Output 1
5
Sample Input 2
1 2 0 1 2 3
Sample Output 2
4
