Рабочее место участника

Fiona designs a new computer game Froggy Ford. In this game, a player helps a frog to cross a river using stone fords. Frog leaps from the river's shore to the first stone ford, than to the second one and so on, until it reaches the other shore. Unfortunately, frog is pretty weak and its leap distance is quite limited. Thus, a player should choose the optimal route – the route that minimizes the largest leap required to traverse the route.

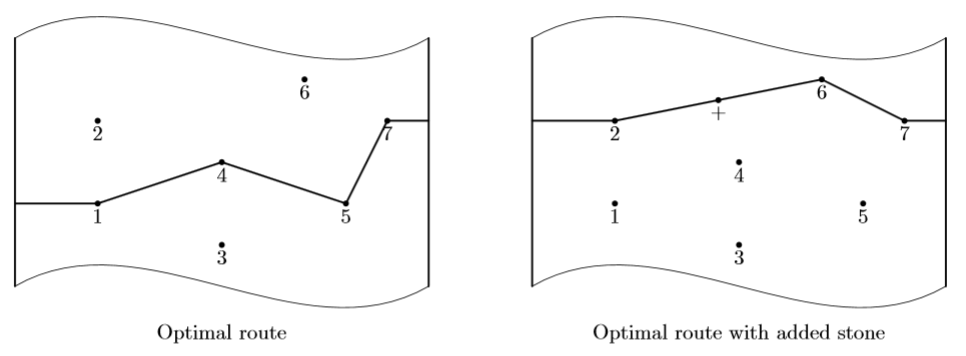
Fiona thinks that this game is not challenging enough, so she plans to add a possibility to place a new stone in the river. She asks you to write a program that determines such a location of the new stone that minimizes the largest leap required to traverse the optimal route.

The first line of the input file contains two integers `w` – the width of the river and `n` – the number of stones in it (`1\ ≤\ w\ ≤\ 10^9`, `0\ ≤\ n\ ≤\ 1000`).

Each of the following `n` lines contains two integers `x_i`, `y_i` – the coordinates of the stones (`0\ <\ x_i\ <\ w`, `-10^{9}\ ≤\ y_i\ ≤\ 10^9`). Coordinates of all stones are distinct.

River shores have coordinates `x=0` and `x=w`.

Write to the output file two real numbers `x_+` and `y_+` (`0\ <\ x_+\ <\ w`, `-10^{9}\ ≤\ y_+\ ≤\ 10^9`) – the coordinates of the stone to add. This stone shall minimize the largest leap required to traverse the optimal route. If a new stone cannot provide any improvement to the optimal route, then an arbitrary pair of `x_+` and `y_+` satisfying the constraints can be written, even coinciding with one of the existing stones.

Your answer shall be precise up to three digits after the decimal point.

10 7
2 2
2 4
5 1
5 3
8 2
7 5
9 4

4.5 4.5