Начало
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
Задачи
2236. Матрица в многомерном пространстве
Поиск в ширину (BFS)Олимпиадные задачи на русском языке
| 17/10/2015 | Личные соревнования по спортивному программированию (A) |
Ограничения: время – 500ms/1000ms, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
В некотором многомерном подпространстве путешествует невырожденная матрица размера 3x3,
двигаясь только вертикально или горизонтально. Она должна найти путь к выходу из подпространства,
который всегда существует. В случае, если матрица встречает препятствие, которое не может обойти в
полном виде, то она может сжаться до одного единственного собственного значения и продолжить весь оставшийся путь
в таком виде. Матрица сжимается относительно центральной клетки, после сжатия размер матрицы становится 1x1.
В сжатом виде шаги матрицы становятся медленнее в 9 раз. Сжатие матрицы происходит мгновенно, то есть без
затрат времени. Необходимо определить наименьшее время, необходимое для выхода из подпространства.
В первой строке ввода содержится 6 целочисленных значений, разделенных пробелами:
координаты `X`, `Y` начального положения центральной ячейки матрицы, координаты `X`, `Y` выхода из подпространства
(все координаты вычисляют с 0, начало координат находится в левом верхнем углу),
ширина `W` и высота `H` подпространства (`3\ ≤\ H,\ W\ ≤\ 200`).
В следующих `H` строчках описывается карта подпространства: символу '.' соответствует свободная
клетка подпространства, символу '#' соответствует преграда.
В начальной положении препятствий в соседних с центром матрицы клетках нет.
Вывести одно целое число – минимальное время для выхода матрицы из подпространства.
Для выхода из подпространства центр матрицы должен оказаться в клетке, соответствующей выходу.
Один шаг матрицы в несжатом виде занимает 1 единицу времени, один шаг в сжатом виде – 9 единиц времени.
Пример ввода
1 5 10 5 11 11 ###........ ##....#.... #.......... ......##... .....##.... ....##..... .....##.... ......##... #......##.. ##......##. ###......##
Пример вывода
87
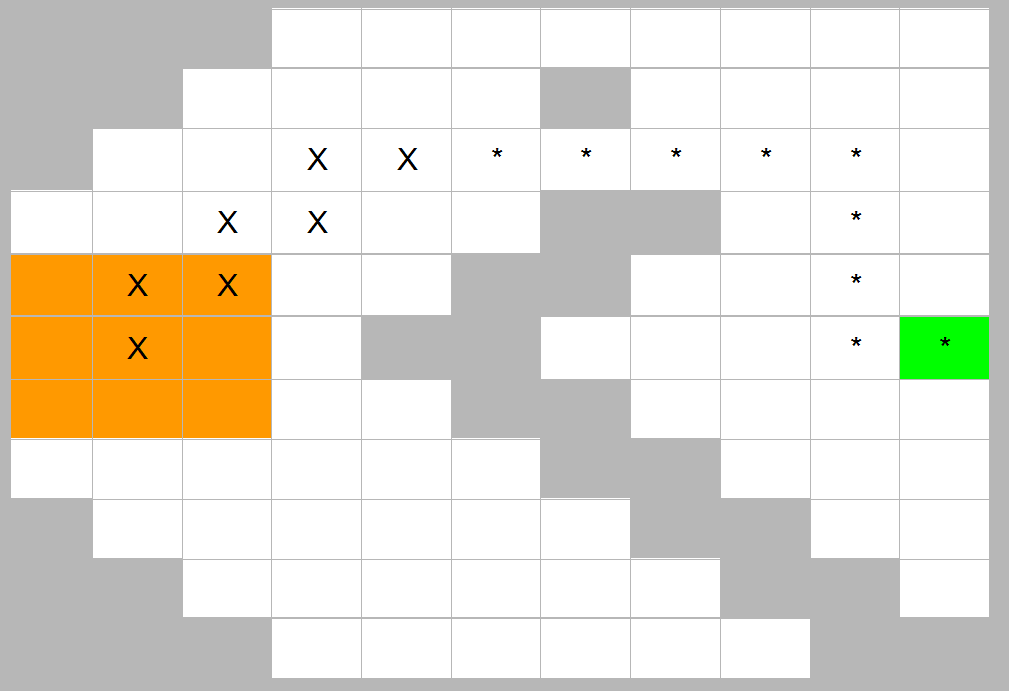
На рисунке символами 'X' отмечен путь перемещения центра матрицы в несжатом виде, а символами '*' – путь перемещения матрицы в сжатом виде.
