Рабочее место участника

This is an interactive problem.

Gomoku is a two-player game on a two-dimensional grid. Each cell of the grid can be either empty, contain the first player’s mark (black), or contain the second player’s mark (white), but not both. Initially the entire grid is empty. Two players make alternating moves, starting with the first player. At each move, a player can put her mark into exactly one empty cell. The first player to have her five adjacent marks in a single row wins. The winning row can be either vertical, horizontal or diagonal.

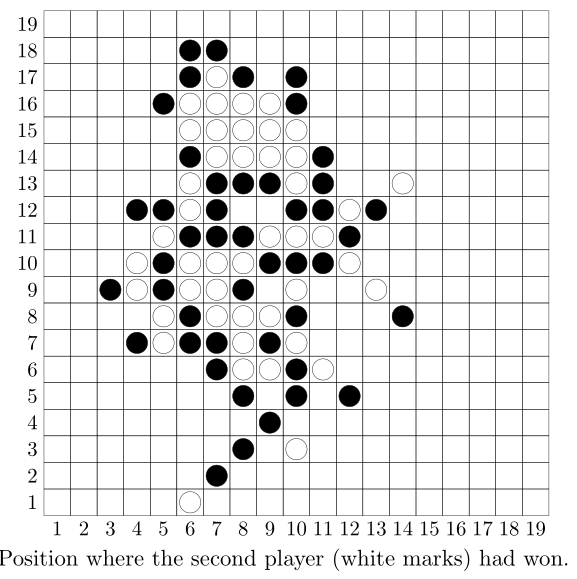
The players use a `19\ "xx"\ 19` grid in this problem. If the entire grid gets filled with marks but no player has won, the game is declared a draw.

The first player uses the following strategy: as the first move, she puts her mark into the center cell of the grid. At every other move, she picks such a move that maximizes the score of the resulting position.

In order to find the score of a position, the first player considers all possible places where the winning combination might eventually form — in other words, all horizonal, vertical and diagonal rows of five consecutive cells on the board (of course, they may overlap each other). If such a row contains both the first player’s marks and the second player’s marks, it is disregarded. If such a row contains no marks, it is disregarded as well. For each row with exactly `k` (`1\ ≤\ k\ ≤\ 5`) marks of the first player and no marks of the second player, add `50^{2k-1}` to the score of the position. For each row with exactly `k` marks of the second player and no marks of the first player, subtract `50^{2k}` from the score of the position. Finally, add a random integer number between 0 and `50^2\ -\ 1` to the score. This random number is chosen uniformly.

In case when several moves of the first player have equal scores (such ties are quite rare because of the random addition mentioned above), the first player picks the one with the smallest `x`-coordinate, and in case of equal `x`-coordinates, the one with the smallest `y`-coordinate.

Your task is to write a program that plays the second player and beats this strategy.

Your program will play 100 games against the strategy described above, with different seeds of random generator. Your program must win all these games.

On each step, your program must:

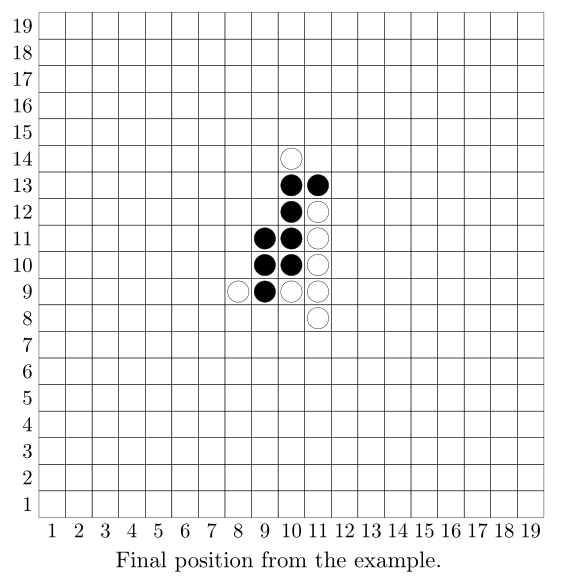
In the example below the first player does not use the strategy from the problem statement. The example is given only to illustrate the interaction format.

10 10
10 11
10 12
10 13
9 10
9 11
9 9
11 13
-1 -1

11 10
11 11
10 9
10 14
8 9
11 9
11 12
11 8