 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
2211. Укладка плитки Динамическое программирование и запоминающие функции
Динамическое программирование и запоминающие функцииОлимпиадные задачи на русском языке

| 26/01/2015 | Региональный этап олимпиады школьников по информатике. II тур. (7) |
| 18/11/2023 | Марафон 80 задач, 5 этап (H) |
Ограничения: время – 1s/2s, память – 256MiB Ввод: tiling.in или стандартный ввод Вывод: tiling.out или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
В процессе ремонта в Лаборатории Информационных Технологий строителям необходимо заменить поврежденные
напольные плитки в коридоре лаборатории, который имеет размер `2 times n` метров. В распоряжении строителей
есть неограниченный запас плиток двух размеров: `1 times 2` метра и `1 times 1` метр. При этом плитки
размером `1 times 2` метра перед укладкой разрешается поворачивать на 90 градусов и размещать как
вдоль, так и поперек коридора.
Строители уже начали ремонт и уложили в некоторых местах пола коридора `k` плиток размером `1 times 1`. Для
завершения ремонта прорабу необходимо подготовить план дальнейших работ. Для этого ему надо решить, каким
образом уложить плитки на места, где они еще не уложены. Это можно сделать различными способами и
прораб хочет перебрать все варианты и выбрать самый удачный. Перед тем как
это сделать, прораб хочет знать, какое количество вариантов ему придется рассмотреть. Это число
требуется найти по модулю `10^9 + 7`.
Требуется написать программу, которая по заданной длине коридора n и расположению плиток,
которые уже уложены, определяет количество способов укладки плиток на оставшиеся места.
Ответ необходимо вывести по модулю `10^9 + 7`.
Формат входного файла
Первая строка входного файла содержит два целых числа: `n` - длину коридора и
`k` - количество уже уложенных единичных плиток (`1 ≤ n ≤ 100 000`, `0 ≤ k < 2n`).
Последующие `k` строк содержат по два целых числа `x_i` и `y_i`, которые задают позиции уже уложенных
единичных плиток, `i`-я плитка уложена на `x_i`-м метре коридора в `y_i`-м ряду (`1 ≤ x_i ≤ n`, `1 ≤ y_i ≤ 2`).
Формат выходного файла
Выходной файл должен содержать одно целое число – количество способов укладки плиток
в коридоре, взятое по модулю `10^9 + 7`.
Пример ввода 1
2 0
Пример вывода 1
7
Пример ввода 2
3 0
Пример вывода 2
22
Пример ввода 3
3 1 2 1
Пример вывода 3
8
Пояснения к примерам
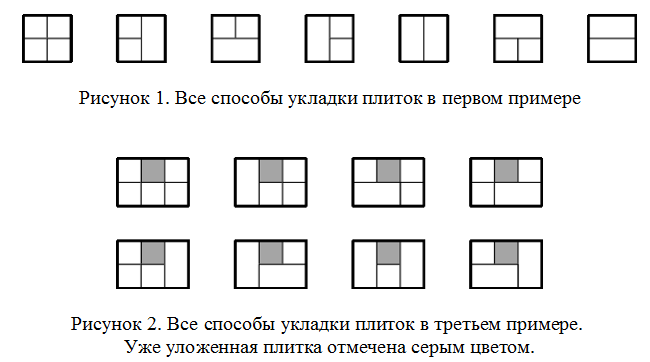
Внимание! Третий тест не подходит под ограничения для
первых трех подзадач, но решение принимается на проверку только в том случае, если оно
выводит правильный ответ на все тесты из примера. Решение должно выводить правильный ответ
на третий тест даже, если оно рассчитано на решение только каких-либо подзадач из первых трех.
Система оценки и описание подзадач
Подзадача 1 (20 баллов)
`1 ≤ n ≤ 8`, `k\ =\ 0`
Баллы за подзадачу начисляются только в случае, если все тесты подзадачи пройдены.
Подзадача 2 (20 баллов)
`1 ≤ n ≤ 1000`, `k\ =\ 0`
Баллы за подзадачу начисляются только в случае, если все тесты подзадачи пройдены.
Подзадача 3 (20 баллов)
`1 ≤ n ≤ 100 000`, `k\ =\ 0`
Баллы за подзадачу начисляются только в случае, если все тесты подзадачи пройдены.
Подзадача 4 (40 баллов)
`1 ≤ n ≤ 100 000`, `1 ≤ k ≤ 2n`
В этой подзадаче 20 тестов, каждый тест оценивается в 2 балла. Баллы за каждый тест начисляются независимо.
Получение информации о результатах окончательной проверки
По запросу сообщается результат окончательной проверки на каждом тесте.
Источник: региональный этап Всероссийской олимпиады по информатике 2014/2015, http://neerc.ifmo.ru/school/  Начало
Начало