 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
2207. Река Дерево отрезков, декартово дерево, √-декомпозиция
Дерево отрезков, декартово дерево, √-декомпозицияОлимпиадные задачи на русском языке

| 24/01/2015 | Региональный этап олимпиады школьников по информатике. I тур. (3) |
| 07/02/2015 | STL 1: vector (C) |
Ограничения: время – 1s/2s, память – 256MiB Ввод: river.in или стандартный ввод Вывод: river.out или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Во Флатландии протекает богатая рыбой река Большой Флат. Много лет назад река была поделена
между `n` рыболовными предприятиями, каждое из которых получило непрерывный отрезок реки. При этом `i`-е предприятие,
если рассматривать их по порядку, начиная от истока, изначально получило отрезок реки длиной `a_i`.
С тех пор с рыболовными предприятиями во Флатландии `k` раз происходили различные события.
Каждое из событий было одного из двух типов: банкротство некоторого предприятия или разделение
некоторого предприятия на два.
При некоторых событиях отрезок реки, принадлежащий предприятию, с которым это событие происходит, делится
на две части. Каждый такой отрезок имеет длину большую или равную 2. Деление происходит
по следующему правилу. Если отрезок имеет четную длину, то он делится на две равные части. Иначе он
делится на две части, длины которых различаются ровно на единицу, при этом часть, которая ближе
к истоку реки, имеет меньшую длину.
При банкротстве предприятия происходит следующее. Отрезок реки, принадлежавший обанкротившемуся
предприятию, переходит к его соседям. Если у обанкротившегося предприятия один сосед, то этому соседу
целиком передается отрезок реки обанкротившегося предприятия. Если же соседей двое, то отрезок реки
делится на две части описанным выше способом, после чего каждый из соседей присоединяет к
своему отрезку ближайшую к нему часть.
При разделении предприятия отрезок реки, принадлежавший разделяемому предприятию, всегда делится на
две части описанным выше способом. Разделившееся предприятие ликвидируется, и образуются два новых предприятия.
Таким образом, после каждого события каждое предприятие владеет некоторым отрезком реки.
Министерство финансов Флатландии предлагает ввести налог на рыболовные предприятия, пропорциональный
квадрату длины отрезка реки, принадлежащего соответствующему предприятию. Чтобы
проанализировать, как будет работать этот налог, министр хочет по имеющимся данным узнать, как
изменялась величина, равная сумме квадратов длин отрезков реки, принадлежащих
предприятиям, после каждого произошедшего события.
Требуется написать программу, которая по заданному начальному разделению реки между
предприятиями и списку событий, происходивших с предприятиями, определит, чему равна сумма квадратов
длин отрезков реки, принадлежащих предприятиям, в начальный момент времени и после каждого события.
Формат входного файла
Первая строка входного файла содержит два целых числа: `n` и `p` – исходное количество предприятий
(`2 ≤ n ≤ 100 000`) и номер подзадачи (`0 ≤ p ≤ 4`).
Вторая строка входного файла содержит n целых чисел `a_1,\ a_2,\ …,\ a_n` - длины исходных отрезков реки.
Третья строка входного файла содержит целое число `k` - количество событий, происходивших с
предприятиями (`1 ≤ k ≤ 100 000`).
Последующие `k` строк содержат описания событий, `i`-я строка содержит два целых числа: `e_i` и `v_i` – тип события
и номер предприятия, с которым оно произошло. Значение `e_i = 1` означает, что предприятие, которое после
всех предыдущих событий является `v_i`-м по порядку, если считать с единицы от истока реки, обанкротилось,
а значение `e_i = 2` означает, что это предприятие разделилось на два.
Гарантируется, что значение `v_i` не превышает текущее количество предприятий.
Гарантируется, что если отрезок предприятия при банкротстве или разделении требуется
поделить на две части, то он имеет длину большую или равную 2. Гарантируется, что если на реке
осталось единственное предприятие, оно не банкротится.
Формат выходного файла
Выходной файл должен содержать `(k + 1)` целых чисел, по одному в строке. Первая строка должна
содержать исходную сумму квадратов длин отрезков реки, а каждая из последующих `k` строк – сумму квадратов
длин отрезков реки после очередного события.
Пример ввода
4 0 3 5 5 4 5 1 1 2 1 1 3 2 2 1 3
Пример вывода
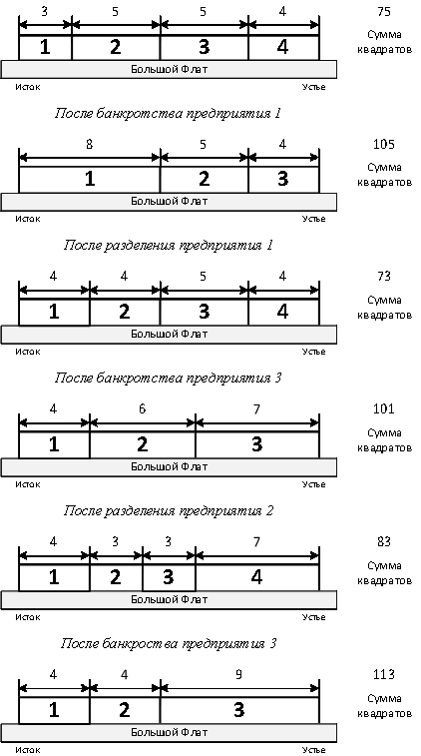
75 105 73 101 83 113
Пояснения к примеру
Распределение отрезков реки между предприятиями после каждого события, описанного в примере, приведено на рисунке ниже.
Система оценки и описание подзадач
В этой задаче четыре подзадачи. Баллы за каждую подзадачу начисляются только в случае, если все тесты для данной подзадачи успешно пройдены.
Внимание! Тест из примера не подходит под ограничение подзадачи 3. Тем не менее, решение задачи принимается на проверку только в том случае, если оно выводит правильный ответ на тесте из примера, даже если участник претендует на правильное решение только этой подзадачи.
В первой строке каждого теста после числа `n` указан номер подзадачи, для теста из
примера указано число 0, в тестах первой подзадачи указано число 1, и т. д.
Подзадача 1 (30 баллов)
`2 ≤ n ≤ 100`, `1 ≤ k ≤ 100`, `1 ≤ a_i ≤ 100`, `p\ =\ 1`
Подзадача 2 (30 баллов)
`2 ≤ n ≤ 100 000`, `1 ≤ k ≤ 100 000`, `1 ≤ a_i ≤ 10^4`, `p\ =\ 2`
Для всех `i` от 1 до `k\ –\ 1` выполнено условие: `|v_i\ –\ v_i\ +\ 1| ≤ 10`
Подзадача 3 (20 баллов)
`2 ≤ n ≤ 100 000`, `1 ≤ k ≤ 100 000`, `1 ≤ a_i ≤ 10^4`, `p\ =\ 3`
Все события имеют тип `e_i = 1` (нет разделений предприятий, только банкротства).
Подзадача 4 (20 баллов)
`2 ≤ n ≤ 100 000`, `1 ≤ k ≤ 100 000`, `1 ≤ a_i ≤ 10^4`, `p\ =\ 4`
Получение информации о результатах окончательной проверки
По запросу сообщается результат окончательной проверки на каждом тесте.
Источник: региональный этап Всероссийской олимпиады по информатике 2014/2015, http://neerc.ifmo.ru/school/  Начало
Начало