 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
2111. Blocks Поиск экстремума функции
Поиск экстремума функцииОлимпиадные задачи на английском языке

| 15/07/2014 | Лето 2014 - 11 (C) |
Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Mirko and Slavko are playing with bricks. Both of them have their own pile of bricks. The piles consist
of `N` columns (where `N` is an odd number). The number of bricks in the `i`th column of Mirko's pile is
labeled with `m_i` and Slavko's pile with `s_i`.
They have decided to create two equal piles constructed in a way that the heights of columns are
strictly descending at first and then strictly ascending (see right image below) and the heights of
adjacent columns differ exactly by 1 (see image). The lowest of the columns must have an equal
number of columns to the left and to the right of it.
The piles can be modified by removing one brick from the top of some column and throw it out the
window (they cannot reuse it) or by taking one brick from the box and place it on the top of some
column (there is an infinite amount of bricks in the box). Removing or placing a brick counts as one
move.
You have to determine the minimal number of moves so that Mirko and Slavko can rearrange their
piles in the described way.[p]
[p=!]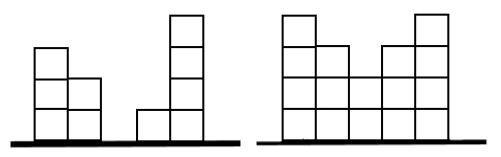

On the left, there is a pile with column heights 3, 2, 0, 1 and 4.
On the right, there is one of the possible final layouts.
The first line of input contains an odd number `N` (`1\ ≤\ N\ ≤\ 300\ 000`), the number of columns in both
piles.
The second line of input contains `N` integers `m_i` (`0\ ≤\ m_i\ ≤\ 10^12`), column heights in Mirko's pile.
The third line of input contains `N` integers `s_i` (`0\ ≤\ s_i\ ≤\ 10^12`), column heights in Slavko's pile.
The first and only line of output must contain the minimal number of moves.
Sample Input #1
3 1 2 3 3 2 2
Sample Output #1
3
Sample Input #2
5 2 3 0 1 4 3 3 2 3 1
Sample Output #2
10
Clarification of the first example: Mirko places two bricks on the top the first column in his pile and
Slavko places one brick on the top of the third column in his pile.
Source: COCI 2013/2014, contest #6 Начало
Начало