 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
2028. Дом Мэра Разбор случаев
Разбор случаевБыстрая сортировка
Олимпиадные задачи на русском языке

| 01/02/2014 | Областная олимпиада школьников по информатике. I тур. (4) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
При планировании нового района города М было решено, что дороги в новом районе будут образовывать прямоугольную сетку, то есть все улицы будут одного из двух типов – направленные с юга на север или направленные с востока на запад. При этом параллельные улицы будут проходить через каждый километр, и каждый квартал будет иметь размер ровно один километр на один километр. Таким образом, все дороги образуют равномерную клетчатую сетку. По каждой дороге разрешен проезд в любом из двух направлений.
Через некоторое время после постройки дорог оказалось, что такая планировка не всегда удобна, поскольку для постройки больших заводов или других сооружений и организации парков недостаточно одного квартала. Мэрия города М решила отдать каждому большому проекту по прямоугольному блоку из нескольких соседних кварталов. К сожалению, после реализации проекта все дороги внутри такого блока будут закрыты для проезда, но по границе блоков проезд все еще будет возможен. Касание двух блоков не закрывает проезд между ними.
Когда Мэру города М принесли на согласование план распределения территорий для больших проектов, ему стало интересно,
насколько сложным будет маршрут от мэрии до его будущего дома. Мэрия находится в центре нового района, на пересечении
нулевой улицы, направленной с юга на север, и нулевой улицы, направленной с востока на запад. С итоговым
расположением дома Мэр еще не определился и на выбор у него есть `k` вариантов. Каждый из вариантов находится
на пересечении `x_i`-ой улицы, направленной с юга на север (положительный `x` означает, что улица находится
восточнее мэрии, отрицательный – западнее) и `y_i`-ой улицы, направленной с востока на запад (положительный `y`
означает, что улица находится севернее мэрии, отрицательный – южнее).
Мэр считает, что маршрут до дома является сложным, если ему на этом маршруте придется совершить более двух
поворотов направо или налево. Машина Мэра не может совершать более одного поворота на перекрестке, например, чтобы
развернуться. Длина маршрута не имеет значения, и к дому можно подъезжать с любой стороны. Машина Мэра
всегда стоит у мэрии в северном направлении, может повернуть сразу направо или налево, но не может развернуться.
Требуется написать программу, которая по информации о закрытых для проезда блоках кварталов и возможным
расположениям дома Мэра, для каждого возможного расположения дома Мэра найдет несложный маршрут
от мэрии до дома, определит кратчайший из них, или сообщит, что такого маршрута не существует. Количество
поворотов минимизировать не требуется.
Формат входного файла
Первая строка входного файла содержит два целых числа `n` и `k` (`0 ≤ n ≤ 100 000`, `1 ≤ k ≤ 10`) – количество
блоков кварталов, которые по плану будут отданы большим проектам и количество вариантов расположения дома Мэра, соответственно.
Последующие `n` строк содержат по описанию блоков кварталов – четыре целых числа `u_1,\ v_1,\ u_2,\ v_2` (`–10^9 ≤ u_1 < u_2 ≤ 109`, `–10_9 ≤ v1 < v2 ≤ 10_9`) —
номера улиц, на пересечении которых расположены противоположные углы блока кварталов, отданных под застройку и закрытых для проезда.
Последующие последние `k` строк содержат по два целых числа `x_i` и `y_i` (`|xi| ≤ 10^9`, `|"yi"| ≤ 10^9`, `x_i ≠ 0`
или `y_i ≠ 0`) — возможные расположения дома Мэра.
Мэрия и никакое из возможных расположений дома Мэра не находятся внутри блоков кварталов, отданных под застройку, но
блоки кварталов, отданные под застройку, могут пересекаться.
Формат выходного файла
В выходной файл для каждого из возможных расположений дома Мэра в порядке появления во входном файле
необходимо вывести сообщение, существуют ли несложный маршрут от мэрии до дома Мэра и, если существует, то
где надо сделать повороты.
Если не существует несложный маршрут, то сообщение должно содержать слово NO на одной строке.
Иначе, в первой строке должно содержаться слово YES, во второй строке – одно число `t` (`0 ≤ t ≤ 2`) – количество
поворотов, и в последующих `t` строках – описания поворотов в порядке их совершения: в каждой строке по
три числа `x`, `y` и `d` – номера улиц, на которых расположен перекресток, где необходимо повернуть, и направление поворота, при этом `d = –1` означает поворот налево и `d = 1` – поворот
направо.
Координаты перекрестков, где необходимо совершить повороты, не должны превышать `10^9`. Если кратчайших
несложных путей несколько, необходимо вывести любой из них.
Пример ввода 1
1 2 -2 1 9 2 2 0 3 3
Пример вывода 1
YES 1 0 0 1 NO
Пример ввода 2
2 1 0 2 2 4 1 0 4 2 3 3
Пример вывода 2
YES 2 0 2 1 3 2 -1
Пример ввода 3
0 2 0 -1 0 1
Пример вывода 3
NO YES 0
Пояснения к примерам
Далее приведен рисунок для второго примера.
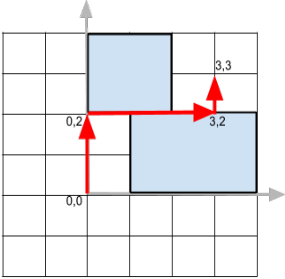
Система оценивания
Частичные правильные решения для тестов, в которых все координаты (`x`, `y`, `u` и `v`) по модулю не превышают 100, и `n ≤ 50`, будут оцениваться из 30 баллов.
Частичные правильные решения для тестов, в которых `n ≤ 50`, будут оцениваться из 60 баллов.
Источник: региональный этап Всероссийской олимпиады по информатике 2013/2014, http://neerc.ifmo.ru/school/  Начало
Начало