 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
2020. ASCII Puzzle Рекурсивный перебор
Рекурсивный переборОлимпиадные задачи на английском языке

| 12/12/2013 | Занятие 12 для продолжающих (Задачи NEERC 2013) (A) |
Ограничения: время – 3s/6s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Fili and Floi play a puzzle game. Fili takes a rectangular piece of paper that is lined with a `W\ times\ H` grid
of square cells, cuts it into pieces on its grid lines, and carefully shuffles the pieces so that pieces do not
rotate. Floi has to recombine the pieces back into the rectangle without rotating them.
Fili observes a number of constraints while cutting an original paper into pieces to make sure that the
resulting puzzle is well-formed. First of all, Fili picks three integer numbers `w`, `h`, and `n`, so that an
original rectangular paper has a width of `W` = `"wn"` cells and a height of `H` = `"hn"` cells. Here `w` and `h` are
known to Floi, but `n`, `W`, and `H` are not. This way, the original rectangular piece of paper can be cut
into a trivial puzzle of `k\ =\ n^2` rectangles with a width of `w` cells and a height of `h` cells each. However,
this trivial puzzle for `k\ >\ 1` is not considered a well-formed puzzle for this game. Instead, the pieces into
which the original rectangle is cut are based on these trivial `w\ times\ h` cell rectangles with the jagged edges
between the adjacent pieces. Formally, the pieces into which the original `W\ times\ H` paper is cut satisfy the
following constraints of a well-formed puzzle:
- There are `k\ =\ n^2` pieces.
- Each piece is a simple 4-connected region of cells without holes.
- Each cell of the original rectangular `W\ times\ H` paper is a part of exactly one piece.
- Each piece contains four corners of the corresponding `w\ times\ h` rectangle in the trivial puzzle for the original paper.
- The cells of each piece can come only from the corresponding `w\ times\ h` rectangle in the trivial puzzle, from the cells adjacent to this rectangle, and from the interior cells of the adjacent rectangles in the trivial puzzle.
- The cut between two adjacent pieces cannot be straight. Only pieces that lie on the border of the original `W\ times\ H` paper have straight sides.
The corollary of these constraints is that each piece of a well-formed puzzle fits into a rectangle of
`(3w\ -\ 2)\ times\ (3h\ -\ 2)` cells. Moreover, the description of each piece will be given as a `(3w\ -\ 2)\ times\ (3h\ -\ 2)`
grid of cells in such a way, that the corresponding `w\ times\ h` rectangle of the trivial puzzle is exactly in the center.
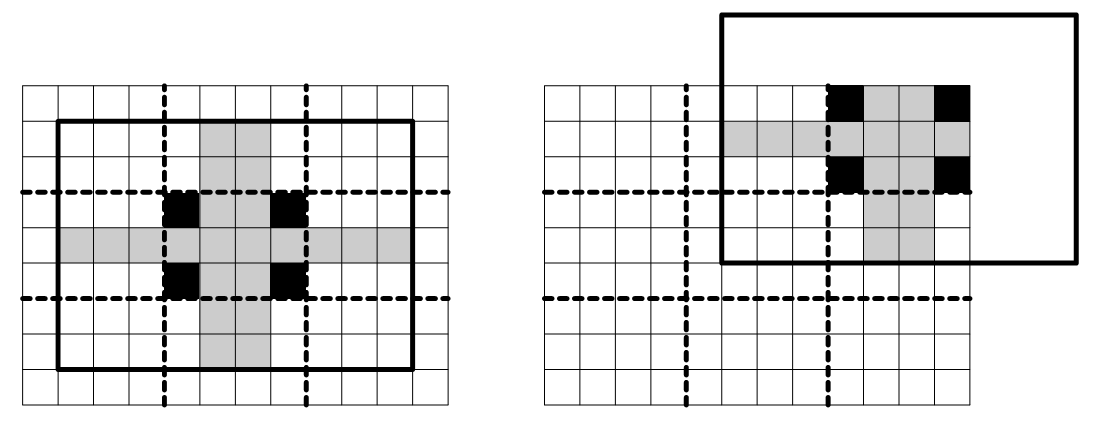
The picture below to the left shows a sample rectangular piece of paper that is lined with a `W\ times\ H\ =\ 12\ times\ 9`
square grid of cells and is cut into a trivial puzzle of `k\ =\ 9` rectangles with a width of `w\ =\ 4` cells and
a height of `h\ =\ 3` cells each with bold dashed lines. The corners of the central `3\ times\ 4` piece of this trivial
puzzle are shown in black. They have to be a part of the central piece of any well-formed puzzle. The
other potential cells of the central piece of a well-formed puzzle are shown in gray. The bold black line
shows `(3w\ -\ 2)\ times\ (3h\ -\ 2)\ =\ 10\ times\ 7` rectangular region that will be describing this central piece. The
picture to the right shows the same for the piece in the upper-right corner of the puzzle.
Your task is to help Floi solve the puzzle.
Input
The first line of the input file contains there integers `k`, `w` and `h`. Here `k` is the number of pieces in the
puzzle, `w` is a width and `h` is a height of a trivial puzzle piece (`k\ =\ n^2` for `1\ ≤\ n\ ≤\ 4`, `3\ ≤\ w,\ h\ ≤\ 5`).
The rest of the input file contains descriptions of `k` pieces of a well-formed puzzle. Each piece is described
by `3h-2` lines that contain `3w-2` characters each. Pieces are labeled with a consecutive English letters
in uppercase (1st piece – 'A', 2nd piece – 'B', and etc). Each piece description uses only two characters
on its `3h-2` lines of `3w-2` characters. The English letter corresponding to the piece denotes a cell that
is a part of this piece, while '.' (dot) character denotes a cell that is not.
Empty lines separate different pieces.
Output
The first line of the output file shall contain `W` and `H` – the size of the original piece of paper that was
cut into the puzzle pieces. The following `H` lines shall contain `W` English letters each, describing the
solution of the puzzle. Letters denote the cells that belong to the corresponding puzzle pieces. If there
are multiple ways to solve the puzzle, then print any solution.
Sample Input
4 4 3 .......... .......... ...AAAA... ...AAAAAA. ...A.AA... .......... .......... .......... .......... ...BBBB... .....BB... ...BBBB... ....BB.... .....B.... .......... .......... ...C..C... ..CCC.C... ...CCCC... .......... .......... .......... ....D..... ...DDDD... ...DDD.... ...DDDD... .......... ..........
Sample Output
8 6 AAAABBBB AAAAAABB ADAABBBB DDDDCBBC DDDCCCBC DDDDCCCC
 Начало
Начало