Рабочее место участника

MegaCity of the future is a rectangular grid of streets. Each intersection has integer Cartesian coordinates `x` and `y`. To get from intersection `a` with coordinates `x_a`, `y_a` to intersection `b` with coordinates `x_b`, `y_b` you need to drive exactly `|x_a-x_b|\ +\ |y_a-y_b|` blocks. Usually, it takes 10 time units to drive one block, so one can easily compute the time it takes to get from `a` to `b`. However, traffic jams that occur in MegaCity turn estimation of minimal driving time into a complex problem that you have to solve.

Traffic jams in MegaCity affect a rectangular area that is specified by coordinates of its bottom-left and top-right corners. The time to travel one block in the traffic jam is specified. All streets that are strictly inside the rectangular region are affected by the traffic jam. Sometimes, it is better to drive around the traffic jams to save time, but sometimes it is better to drive through some traffic jams as shown in the example — 17 blocks are driven outside of traffic jams, taking 10 time units per block, and 2 blocks in the light traffic jam with 11 time units per block.

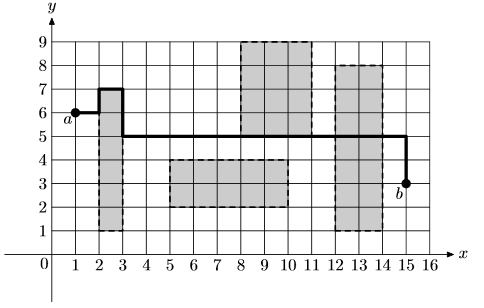
The first line of the input file contains four integer numbers `x_a`, `y_a`, `x_b`, and `y_b` — coordinates of the start and finish intersections. The second line of the input file contains a single integer number `n` (`0\ ≤\ n\ ≤\ 1000`) which specifies the number of traffic jams. The following `n` lines describe traffic jams. Each traffic jam is described by five integer numbers `x_{1,i}`, `y_{1,i}`, `x_{2,i}`, `y_{2,i}` and `t_i`, where first four numbers are coordinates of the bottom-left and top-right corners of the jammed area (`x_{1,i}\ <\ x_{2,i}`, `y_{1,i}\ <\ y_{2,i}`), and `t_i` (`10\ <\ t_i\ ≤\ 10^8`) is the time it takes to travel one block inside this traffic jam. All coordinates in the input file are from 0 to `10^8` inclusive. Areas of traffic jams neither intersect nor touch each other. Start and finish points are different and do not lie inside nor on the border of any traffic jam.

Write to the output file a single integer — the minimal driving time from intersection `a` to intersection `b`.

1 6 15 3
4
2 1 3 7 44
5 2 10 4 33
8 5 11 9 22
12 1 14 8 11

192