Рабочее место участника

Как известно, любую логическую функцию от `N` переменных можно реализовать цифровой электронной схемой, используя только логические элементы "И-НЕ".

Примечание: логический элемент "И-НЕ" выполняет операцию "логическое И" над входными сигналами и инвертирует результат.

На практике желательно учитывать, что реальные логические элементы обрабатывают смену входных сигналов с некоторой задержкой. Соответственно, при последовательном подключении элементов (т.е. выход первого на вход второго) эта задержка суммируется.

Требуется написать программу, строящую схему для заданной логической функции `f(x_1,…,\ x_N)`. Построенная схема должна обладать минимальной задержкой — то есть путь максимальной длины от одного из входов схемы к её выходу должен быть как можно короче.

Схема должна представлять собой ациклический ориентированный граф с тремя типами вершин:

1. Вершины-элементы "И-НЕ". В каждую такую вершину должно входить ровно две дуги, а выходить может одна или более (тем самым обеспечивается возможность разветвления выходного сигнала). Данные вершины нумеруются последовательными целыми числами 1, 2, …, `M` (где `M` — общее количество элементов "И-НЕ").

2. `N` вершин-входов. В данные вершины не должны входить дуги, а выходить из каждой может ноль и более дуг. Данные вершины нумеруются отрицательными целыми числами от `–N` до `–1`. Каждой входной переменной `x_i` соответствует вершина с номером `–i`.

3. Одна вершина-выход. Из неё не должны выходить дуги, а входить в неё должна ровно одна дуга. Данная вершина имеет номер 0.

Несложно заметить, что общее количество дуг в таком графе будет равняться `2*M\ +\ 1`.

В первой строке входного файла записано целое число `N` — количество переменных (`1\ ≤\ N\ ≤\ 3`). В следующей строке через пробел записаны `2^N` чисел 0 или 1 — значения функции `f` на каждом возможном наборе входных переменных `x_1,\ …,\ x_N` (наборы упорядочены лексикографически).

В первой строке выходного файла выведите через пробел два целых числа `M` и `Q`, где `M` — количество использованных элементов "И-НЕ" (`0\ ≤\ M\ ≤\ 100`), `Q` — количество элементов "И-НЕ" в максимальном пути в графе. В каждой из следующих `2*M+1` строк выведите через пробел два целых числа в диапазоне от `–N` до `M` — начало и конец очередной дуги. Если имеется несколько верных ответов, то выведите любой, дуги можно выводить в любом порядке.

3
0 0 1 1 1 1 1 1

3 2
-2 2
-2 2
-1 3
-1 3
2 1
3 1
1 0

1
0 1

0 0
-1 0

Построенная для функции в первом примере схема изображена на рисунке.

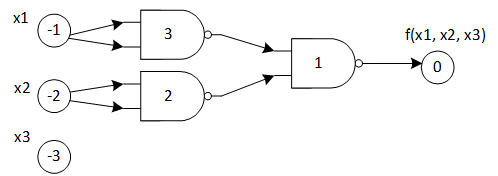
Во втором примере не используется ни одного элемента "И-НЕ" — входной сигнал `x_1` подключен сразу к выходу схемы.