04/12/2024 13:26:06

Рабочее место участника

Выбрать соревнование

Задачи

Послать решение

Результаты проверки

Статистика по задачам

Вопросы и ответы

Результаты соревнования

Задачи

1942. Voyager

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

The Voyager 1 space probe (not to be confused with the Intrepid-class starship) was launched a long time ago, in 1977, and is currently on the verge ofleaving our Solar System. As it travels further through space, it has been programmed to leave a radio signal message in any star system it stumbles upon, to mark the probe's path for as long as possible.

Let us assume that a star system can be representedby a rectangular grid with `N` rows and `M` columns, dividing the space into `N` by `M` equal cells. Each cell can contain a single planet, black hole, or be empty. The probe broadcasts the signal from a pre-determined empty cell, in one of the four axis-aligned directions (“U”-up, “R”-right, “D”-down, “L”-left).

Upon being broadcast, the signal propagates in a straight line along the same row/column until it reaches a planet, where it is deflected by 90 degrees in another direction. There are two kinds of planets, which we will denote by „/“ and „\“. The deflection rules are shown in the image below:

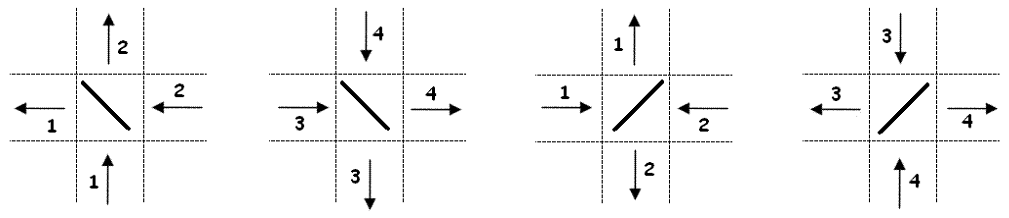
The signal permanently leaves the system upon either entring a cell containing a black hole, or propagating outside the edges of the rectangular grid. It is also known that the signal needs one second to propagate from the current cell to a neighbouring one.

Write a program to determine the direction in which the probe needs to broadcast the signal so that it remains within the system for as long as possible, outputting the optimal direction as well as the resulting longest time. If it is possible for the signal to remain in the system indefinitely, output the message „Voyager“ instead of the required time.

The first line of input contains two positive integers, `N` (`1\ ≤\ N\ ≤\ 500`) and `M` (`1\ ≤\ M\ ≤\ 500`). Each of the following `N` lines contains `M` characters from the set {“/”, “\”, “C”, “.”}, where “/” and “\” represent the two kinds of planets, “C” represents a black hole, and “.” represents an empty cell.

The last line of input contains two positive integers, `"PR"` (`1\ ≤\ "PR"\ ≤\ N`) and `"PC"`(`1\ ≤\ "PC"\ ≤\ M`), the row and column number, respectively, of the cell where the probe is situated.

The first line of output must contain the required optimal broadcast direction (“U”, “R”, “D”, or “L”). If the solution is not unique, select the first optimal one in the following priority order: first “U”, then “R”, then “D”, and finally “L”.

The second line of output must contain the required longest time (or message).

Sample Input #1

5 5
../.\
.....
.C...
...C.
\.../
3 3

Sample Output #1

U 
17

Sample Input #2

5 5
....\
\..\.
./\..
\../C
.\../
1 1

Sample Output #2

D
12

Sample Input #3

5 7
/.....\
../..\.
\...../
/.....\
\.\.../
3 3

Sample Output #3

R
Voyager

Clarification of the first example ("*" represents the path of the singal):

start     'U' direction  'R' direction  'D' direction  'L' direction  
../.\     *.***          ../.\          ../.\          ../.\          
.....     *.*.*          .....          .....          .....          
.CS..     *C*.*          .C***          .C*..          .C*..          
...C.     *..C*          ...C.          ..*C.          ...C.          
\.../     *****          \.../          \.*./          \.../          
          17 seconds     3 seconds      3 seconds      1 second

Source: COCI 2012/2013, contest #4