images/home.png Начало
Имя: Пароль:
Зарегистрироваться
Восстановить пароль
02/05/2024 23:49:05

printРабочее место участника

Выбрать соревнование Задачи Послать решение Результаты проверки Статистика по задачам Вопросы и ответы Результаты соревнования Состояние сервера Изменить данные Управление командой Помощь

printЗадачи

1932. Chains

Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

Mirko has found `N` chains in his attic. Each chain consists of some number of links, where each link has at most two adjacent links. Each link can be opened or closed, so it is possible to separate chains or connect them into a longer chain. Mirko would like to connect all chains into one huge chain, while opening and closing as few links as possible.
For example, if Mirko has only three chains, each consisting of only one link, he can open one of them, use it to connect the remaining two and close it:

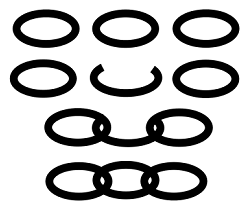
25966.png

Given the number of chains and the length of each chain, find the minimum number of links that Mirko has to open and close in order to bind them all in darkness one long chain.
The first line of input contains the positive integer `N` (`2\ ≤\ N\ ≤\ 500\ 000`), the number of chains. The second line of input contains `N` positive integers `L_i` (`1\ ≤\ L_i\ ≤\ 1\ 000\ 000`), the lengths of individual chains.
The first and only line of output must contain the required minimum number of links.

Sample Input #1

2
3 3

Sample Output #1

1

Sample Input #2

3
1 1 1

Sample Output #2

1

Sample Input #3

5
4 3 5 7 9

Sample Output #3

3
Clarification of the first example: Mirko can open the last link of the first chain, connect it with the first link of the second chain and close it.
Clarification of the third example: Here it is best to completely take apart the chain of length 3, using its three links to connect the remaining chains.
Source: COCI 2012/2013, contest #2
loading