 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
1916. Transformation of the Graph Графы
ГрафыОлимпиадные задачи на английском языке

| 25/04/2003 | 7-й Чемпионат Урала. 2 тур (7) |
| 08/07/2013 | Лето 2013-5 (G) |
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Let find the path going through all the vertices of the oriented graph
one time, i.e. find Hamiltonian path. This problem belongs to the class of NP-hard problems, and its
straightforward solution needs many hours of calculations. Sometimes it's possible to build new graph G', which
contains as mush arcs, as many vertices are in source graph `G`, and there is bijection `φ` (one-to-one
correspondence) between the set of the vertices of `G` and the set of the arcs of `G'` such that if there is an
arc `(x\ y)` in `G`, where `x≠y`, then the end of the arc `φ(x)` in `G'` coincides with the beginning
of the arc `φ(y)`. The bijection `φ` maps adjacent vertices in `G` to adjacent arcs in `G'` and
nonadjacent vertices in `G` to nonadjacent arcs in `G'`. In this case the problem of finding Hamiltonian path
in source graph reduces to the problem of finding Eulerian path in new graph, the last one is much easier.
The self-adjacency of vertices in the source graph and arcs in the new graph should not be taken into account, as
it has not effect to path searching.
Write the program, which checks the possibility of mentioned transformation for given oriented graph and
build new oriented graph.
Input
The first line of the input file contains two integers `K` and `N` (`1\ ≤\ K\ ≤\ 100`, `1\ ≤\ N\ ≤\ K^2`), separated by
space, where `K` is quantity of vertices and `N` is quantity of arcs of source graph `G`. The following `N` lines
contain pairs of integers from 1 to `K`, separated by space; each pair describes the beginning and the end of an arc.
Output
The output file contains zero in case of impossibility of mentioned transformation. Else the first
line contains the quantity `M` of vertices of new graph and the following `K` lines contain information
about arcs of new graph; you should write in `i`-th line the numbers of beginning and end of `i`-th arc, which
corresponds to `i`-th vertex of source graph. Use arbitrary indexing from 1 up to `M` for vertices of new graph.
Sample Input #1
8 16 1 1 1 2 2 4 2 3 3 6 3 5 4 8 4 7 6 3 6 4 5 1 5 2 7 6 7 5 8 8 8 7
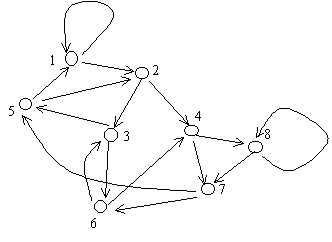
Sample Output #1
4 1 1 1 2 2 3 2 4 3 1 3 2 4 3 4 4
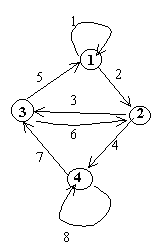
Sample Input #2
3 3 1 2 1 3 2 3
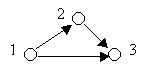
Sample Output #2
3 1 2 2 2 2 3
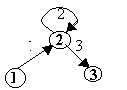
 Начало
Начало