 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
1883. Шифр Полный перебор
Полный переборОлимпиадные задачи на русском языке

| 16/11/2012 | Муниципальный этап 9-11 классы (2) |
| 03/07/2019 | Лето 2019 - 2 (упрощенное) (B) |
| 06/11/2025 | Шифрование ЧОМЛИ 10Б (проводит sartasova) (I) |
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Для открытия замка сейфа в компьютерной игре из серии "Побег из комнаты" нужно найти шифр.
Имеется подсказка – линейка с нанесенными на ней числами, по которой движется ползунок с прорезями,
через которые видны числа на линейке. Края ползунка не могут выйти за границы линейки из-за ограничителей
на концах линейки. Рядом с прорезями на ползунке нарисованы знаки + и есть текст "max". Нетрудно
догадаться, что шифром для сейфа является набор чисел на линейке, видимых через прорези ползунка, сумма
которых максимальна.
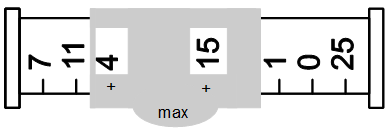
Напишите программу, которая определит шифр для открытия сейфа.
Первая строка ввода содержит одно целое число `N` (`2\ ≤\ N\ ≤\ 10`) – размеры ползунка. Вторая строка
содержит `N` целых чисел от 0 до 1, разделенных пробелами – описание формы ползунка слева направо.
Число 0 означает, что эта часть ползунка не имеет прорезей, а число 1 соответствует части ползунка
с прорезью. В описании ползунка есть по крайней мере одно число 1. Третья строка ввода содержит
одно целое число `M` (`N\ <\ M\ ≤\ 1000`) – количество чисел на линейке. Четвертая
строка ввода содержит `M` целых чисел от 0 до 99, разделенных пробелами – числа на линейке, перечисленные в порядке их размещения на линейке.
Вывести в первой строке `K` целых чисел, разделяя их пробелами – шифр для открытия сейфа, где `K` – количество
прорезей на ползунке. Числа вывести в том порядке, в котором они видны в прорезях ползунка. Если существует
несколько вариантов с максимальной суммой, то вывести вариант, при котором ползунок
расположен левее. Допускается вывод лишних ведущих и завершающих пробелов в строке.
Пример ввода
5 1 0 0 1 0 10 7 11 4 3 5 15 2 1 0 25
Пример вывода
4 15
Пояснение к примеру: Числа, которые появляются в прорезях при движении ползунка
от самой левой возможной позиции до самой правой: 7+3, 11+5, 4+15, 3+2, 5+1, 15+0. Число 25 не может
появиться в прорези ползунка из ограничителей на концах линейки. Максимум суммы чисел в прорезях
достигается на числах 4 и 15.
 Начало
Начало