07/04/2025 07:22:52

Рабочее место участника

Выбрать соревнование

Задачи

Послать решение

Результаты проверки

Статистика по задачам

Вопросы и ответы

Результаты соревнования

Задачи

1854. Расстояния в Плоском мире

Ограничения: время – 1s/2s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод copy
Послать решение Blockly Посылки Темы Где Обсудить (0)

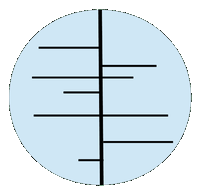
Плоский мир имеет форму диска. Существует только одна дорога, ведущая с севера на юг диска. Эта дорога проходит через центр диска и её называют Осевой. Остальные дороги проложены с запада на восток или с востока на запад от городов Плоского мира до Осевой дороги. Если два города не расположены на одном отрезке дороги, ведущем до Осевой дороги, то, чтобы добраться из одного города в другой, путешественникам нужно сначала дойти до Осевой дороги, затем дойти до дороги, ведущей в нужный город, и затем по ней дойти до города.

Установим систему координат следующим образом. Центр диска имеет координаты

$(0,0)$ . Ось

$Y$ совпадает с Осевой дорогой. Пусть один город имеет координаты

$(X_1,\ Y_1)$ , а другой город – координаты

$(X_2,\ Y_2)$ . Тогда расстояние между городами, у которых

$Y_1\ ≠\ Y_2$ , вычисляется по формуле

$|X_1|\ +\ |X_2|\ +\ |Y_1-Y_2|$ , а расстояние между городами, у которых

$Y_1\ =\ Y_2$ , вычисляется по формуле

$|X_1\ -\ X_2|$ , где

$|a|$ означает абсолютное значение (модуль) числа

$a$ .

Напишите программу, определяющую расстояние, которое нужно пройти по дорогам, чтобы попасть из города с координатами

$(X_1,\ Y_1)$ в город с координатами

$(X_2,\ Y_2)$ .

Формат ввода

Первая строка ввода содержит четыре целых числа

$X_1$ ,

$Y_1$ ,

$X_2$ ,

$Y_2$ (

$0\ ≤\ X_1^2+Y_1^2\ ≤\ 10^8$ ,

$0\ ≤\ X_2^2+Y_2^2\ ≤\ 10^8$ ) – координаты двух городов.

Формат вывода

В первой строке вывести одно целое число – расстояние между городами по дорогам.

Пример ввода

10 15 -10 -5

Пример вывода