 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
1797. Луна Техника программирования, моделирование
Техника программирования, моделированиеОлимпиадные задачи на русском языке

| 25/06/2012 | Лето 2012 - дорешивание ( 9D) |
| 09/07/2012 | Лето 2012 - 9 (D) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Начинающий астроном Даша наконец-то обзавелась цифровым фотоаппаратом.
Конечно, фиксировать звездное небо нажатием кнопки, а уже затем
производить исследования – гораздо удобней.
Разрешающая способность матрицы фотоаппарата оказалась не слишком
высокой, да и на фотографиях ночного неба можно различить только
два цвета: черный и белый. Впрочем, в этом есть и свои плюсы: Даша
сделала уже огромное число снимков, а память все еще не закончилась.
Теперь Дашу интересует положение Луны на каждом из снимков.
Будем считать, что Луна на снимке выглядит как круг с центром в точке
изображения `C` и целым неотрицательным радиусом `r`, то есть как
множество белых точек, расстояние от центров которых до точки
`C` не больше `r`. Луна полностью поместилась на снимке.
Также некоторые достаточно яркие звезды могут присутствовать на снимке
в виде отдельных белых точек. Таких точек не больше `25`.
Объектов, отличных от Луны и звезд, на снимке не изображено.
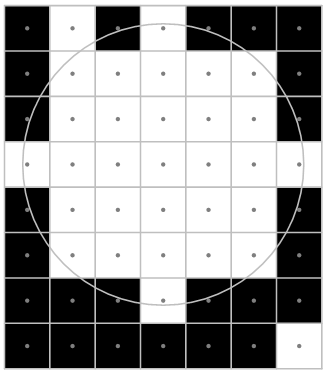
Напишите программу, которая по изображению найдет наибольший
возможный радиус круга, который соответствует Луне, а также ее
возможное положение.
В первой строке ввода записаны целые числа `w` и `h` – горизонтальное и
вертикальное разрешение снимка, соответственно
(`1\ ≤\ w,\ h\ ≤\ 50`).
В следующих `h` строках записано по `w` символов "." (черная
точка) или "*" (белая точка).
В первой строке выведите натуральное число – максимальный радиус изображения Луны. Во второй строке выведите
координаты (столбец, затем строку) центра изображения Луны с данным
радиусом. Столбцы и строки нумеруются с единицы, слева направо и
сверху вниз, соответственно.
Если центров может быть несколько, выведите любой. Гарантируется,
что корректный ответ существует.
Пример ввода 1
7 8 .*.*... .*****. .*****. ******* .*****. .*****. ...*... ......*
Пример вывода 1
3 4 4
Пример ввода 2
5 4 ..... ..... ..*.. .*...
Пример вывода 2
0 2 4
Источник: командный чемпионат школьников Санкт-Петербурга по программированию, 2010
 Начало
Начало