 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
1783. Полярные прямоугольники Геометрия
ГеометрияСортировка
Олимпиадные задачи на русском языке

| 25/06/2012 | Лето 2012 - дорешивание ( 7G) |
| 05/07/2012 | Лето 2012 - 7 (G) |
Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Вася недавно изучил полярную систему координат. А именно, он изучил понятие полярного прямоугольника.
Пусть задана стандартная декартова плоскость. Если на ней нарисовать две окружности с центром в
начале координат, то область, находящаяся между ними, называется кольцом
(на рисунке обозначена синим). Если на ней нарисовать два луча, то область, заметаемая первым
лучом при движении ко второму, называется углом (т.е. область между этими двумя лучами, на
рисунке обозначена зеленым). Полярным прямоугольником называется пересечение некоторого угла
с некоторым кольцом (на рисунке обозначено красным).
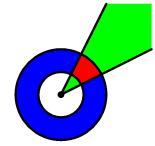
Задано несколько полярных прямоугольников. Найдите площадь их пересечения. Помните, что
пересечение полярных прямоугольников может состоять из нескольких частей!
В первой строке вводится целое число N – количество прямоугольников (`1\ ≤\ N\ ≤\ 5000`).
Далее в `N` строках содержится описание прямоугольников. Каждый прямоугольник описывается
четверкой действительных чисел `r_1,\ r_2,\ phi_1,\ phi_2`, где `r_1,\ r_2` обозначают радиусы окружностей,
образующих кольцо (`r_1\ <\ r_2`), а `phi_1,\ phi_2` обозначают углы, образованные первым и вторым
лучами с осью абсцисс, заданные в радианах. При этом заметается область от первого луча до второго
в направлении против часовой стрелки (т.е. возрастания углов), даже в случае, когда `phi_1\ >\ phi_2`.
Все числа
заданы максимум с шестью знаками после десятичной точки. Углы лежат в полуинтервале `[0;\ 2\ pi)`,
а радиусы не превосходят `10^6`. Гарантируется, что `phi_1\ ≠\ phi_2`.
Выведите единственное число – площадь искомого пересечения. Ответ будет считаться правильным,
если его абсолютная или относительная погрешность не будет превышать `10^{-6}`.
Пример ввода 1
2 1 3 0 3 2 4 1.5 4.5
Пример вывода 1
3.7500000000
Пример ввода 2
2 1 2 0 3 1 2 2 1
Пример вывода 2
3.0000000000
Источник: Московская открытая олимпиада школьников по программированию, 2011/12 учебный год
 Начало
Начало