Рабочее место участника

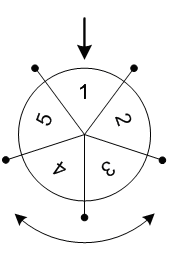
Развлекательный телеканал транслирует шоу "Колесо Фортуны". В процессе игры участники шоу крутят большое колесо, разделенное на сектора. В каждом секторе этого колеса записано число. После того как колесо останавливается, специальная стрелка указывает на один из секторов. Число в этом секторе определяет выигрыш игрока.

Юный участник шоу заметил, что колесо в процессе вращения замедляется из-за того, что стрелка задевает за выступы на колесе, находящиеся между секторами. Если колесо вращается с угловой скоростью `v` градусов в секунду, и стрелка, переходя из сектора `X` к следующему сектору, задевает за очередной выступ, то текущая угловая скорость движения колеса уменьшается на `k` градусов в секунду. При этом если `v\ ≤\ k`, то колесо не может преодолеть препятствие и останавливается. Стрелка в этом случае будет указывать на сектор `X`.

Юный участник шоу собирается вращать колесо. Зная порядок секторов на колесе, он хочет заставить колесо вращаться с такой начальной скоростью, чтобы после остановки колеса стрелка указала на как можно большее число. Колесо можно вращать в любом направлении и придавать ему начальную угловую скорость от `a` до `b` градусов в секунду.

Требуется написать программу, которая по заданному расположению чисел в секторах, минимальной и максимальной начальной угловой скорости вращения колеса и величине замедления колеса при переходе через границу секторов вычисляет максимальный выигрыш.

Первая строка входного файла содержит целое число `n` — количество секторов колеса (`3\ ≤\ n\ ≤\ 100`).

Вторая строка входного файла содержит `n` положительных целых чисел, каждое из которых не превышает 1000 — числа, записанные в секторах колеса. Числа приведены в порядке следования секторов по часовой стрелке. Изначально стрелка указывает на первое число.

Третья строка содержит три целых числа: `a`, `b` и `k` (`1\ ≤\ a\ ≤\ b\ ≤\ 10^9`, `1\ ≤\ k\ ≤\ 10^9`).

В выходном файле должно содержаться одно целое число — максимальный выигрыш.

5
1 2 3 4 5
3 5 2

5

5
1 2 3 4 5
15 15 2

4

5
5 4 3 2 1
2 5 2

5

В первом примере возможны следующие варианты: можно придать начальную скорость колесу равную 3 или 4, что приведет к тому, что стрелка преодолеет одну границу между секторами, или придать начальную скорость равную 5, что позволит стрелке преодолеть 2 границы между секторами. В первом варианте, если закрутить колесо в одну сторону, то выигрыш получится равным 2, а если закрутить его в противоположную сторону, то — 5. Во втором варианте, если закрутить колесо в одну сторону, то выигрыш будет равным 3, а если в другую сторону, то — 4.

Во втором примере возможна только одна начальная скорость вращения колеса – 15 градусов в секунду. В этом случае при вращении колеса стрелка преодолеет семь границ между секторами. Тогда если его закрутить в одном направлении, то выигрыш составит 4, а если в противоположном направлении, то — 3.

Наконец, в третьем примере оптимальная начальная скорость вращения колеса равна 2 градусам в секунду. В этом случае стрелка вообще не сможет преодолеть границу между секторами, и выигрыш будет равен 5.

Правильные решения для тестов, в которых `1\ ≤\ a\ ≤\ b\ ≤\ 1000`, будут оцениваться из 50 баллов.