 Рабочее место участника
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
 Задачи
Задачи
1341. Кубики Вывод формулы
Вывод формулыОлимпиадные задачи на русском языке

| 26/04/1998 | Региональная олимпиада Информатика-1998 (1) |
| 10/09/2011 | Занятие 1 (A) |
Ограничения: время – 200ms/500ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Маленький Метью очень любил играть в кубики.
Он делал столбики из кубиков и ставил эти столбики
на квадратный столик (не случайным образом, а в клетки, если представить
столик разлинованным на клетки по размерам кубиков).
Из-за маленького роста Метью мог построить столбики не
более 8 кубиков. На рисунке можно увидеть одно из его творений
на столике размером 4x4.
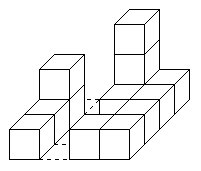
Понравившиеся ему строения он зарисовывал. Но так как он не умел рисовать
3D-изображения, то ограничивался видом спереди и видом справа.
Метью думал, что этой информации достаточно, чтобы построить
это строение снова (но он никогда не пытался сделать это).
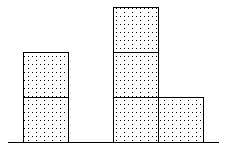 Вид спереди | 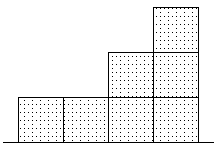 Вид справа |
Через несколько лет, рассматривая рисунки, он понял,
что можно построить более чем одно строение с тем же самым видом
спереди и справа.
Метью обнаружил, что существует
некоторое "минимальное" из всех возможных строение
с минимальным числом кубиков `N` и "максимальное" с числом кубиков `M`.
Для показанного примера "минимальное" строение содержит `N=7` кубиков,
а "максимальное" – `M=17` кубиков.
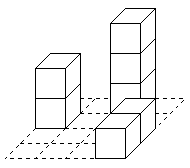 Минимальное строение | 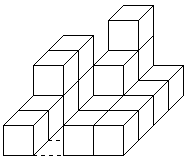 Максимальное строение |
Напишите программу, которая позволяет вычислить
максимальное (`M`) и минимальное (`N`) число кубиков для строения,
задаваемого видами спереди и справа.
Входной файл содержит в первой строке размеры столика `K` (`1\ ≤\ K\ ≤\ 8`),
во второй строке – `K` чисел через пробел: высота столбиков (от 0 до 8)
на виде спереди, в третьей строке также `K` чисел – высота столбиков
на виде справа. Известно, что по этим исходным данным
можно построить как минимум одно строение.
В выходной файл вывести числа `N` и `M` через пробел.
Пример ввода
4 2 0 3 1 1 1 2 3
Пример вывода
7 17
 Начало
Начало