Начало
Рабочее место участника
| Выбрать соревнование | Задачи | Послать решение | Результаты проверки | Статистика по задачам | Вопросы и ответы | Результаты соревнования | Состояние сервера | Изменить данные | Управление командой | Помощь |
Задачи
1293. Inspection
Другие задачи на графыОлимпиадные задачи на английском языке
| 28/11/2009 | Занятие 6 (задачи NEERC 2009) (I) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
You are in charge of a team that inspects a new ski resort. A ski resort
is situated on several mountains and consists of a number of slopes.
Slopes are connected with each other, forking and joining. A map of the
ski resort is represented as an acyclic directed graph. Nodes of
the graph represent different points in ski resort and edges of the graph
represent slopes between the points, with the direction of edges
going downwards.
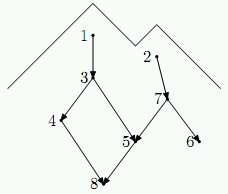
Your team has to inspect each slope of the ski resort. Ski lifts on
this resort are not open yet, but you
have a helicopter. In one flight the
helicopter can drop one person into any point of the resort.
From the drop off point the person
can ski down the slopes, inspecting each slope as they ski.
It is fine to inspect the same slope multiple times, but you have to
minimize the usage of the helicopter. So, you have to figure out how
to inspect all the slopes with the fewest number of helicopter flights.
Input
The first line of the input file contains a single integer number
`n` (`2\ ≤\ n\ ≤\ 100`) – the number of points in the ski resort.
The following `n` lines of the input file describe each point of the ski resort
numbered from `1` to `n`. Each line starts with a single integer
number `m_i` (`0\ ≤\ m_i\ <\ n` for `i` from `1` to `n`) and is followed
by `m_i` integer numbers `a_{{ij}}` separated by spaces. All `a_{{ij}}` are distinct
for each `i` and each `a_{{ij}}` (`1\ ≤\ a_{{ij}}\ ≤\ n`, `a_{{ij}}\ ≠\ i`)
represents a slope going downwards from point `i` to point `a_{{ij}}`.
Each point in the resort has at least one slope connected to it.
Output
On the first line of the output file write a single integer number `k` – the minimal
number of helicopter flights that are needed to inspect all slopes.
Then write `k` lines that describe inspection routes for each helicopter flight.
Each route shall start with single integer number from `1` to `n` – the number
of the drop off point for the helicopter flight, followed by
the numbers of points that will be visited during inspection in the corresponding
order as the slopes are inspected going downwards. Numbers on a line shall
be separated by spaces. You can write routes in any order.
Sample Input
8 1 3 1 7 2 4 5 1 8 1 8 0 2 6 5 0
Sample Output
4 1 3 4 8 1 3 5 8 2 7 6 7 5
