Задачи отборочных командных соревнований школьников 2011

Берляндские ученые вот уже несколько лет занимаются раскопками руин древней цивилизации, существовавшей за века до образования Берляндии и ее соседей и достигшей, по косвенным сведениям, невероятно высокого уровня технологий.

Недавно археологи обнаружили странную находку, предположительно летопись некоторых событий, которая может раскрыть берляндским историкам причину исчезновения столь могущественного общества — стопку из дюжины блестящих тонких дисков из неизвестного материала, нанизанных на алмазный стержень. На верхнем диске ученые обнаружили три числа, каждое из которых состоит из двух цифр. Ученые предположили, что на диске записана дата конца великой цивилизации.

После анализа дисков было установлено, что они использовались в XXI веке по летоисчислению, использовавшемуся древней цивилизацией — так называемому "григорианскому" календарю — год продолжительностью `365` дней, разделялся по нему на двенадцать месяцев. Второй месяц в году имел продолжительность двадцать восемь дней, первый, третий, пятый, седьмой, восьмой, десятый и двенадцатый — тридцать один день, остальные — тридцать дней. В особые года, номер которых делился на четыре и не делился на сто, либо делился на четыреста, второй месяц длился двадцать девять дней. Веком номер `i` назывался период с `100*(i-1)\ +\ 1` года по `100*i`.

Так как достоверно не известно, в каком порядке представители древней цивилизации записывали даты, вам, как главному специалисту по григорианскому календарю, поручили провести исследование — установить, каким датам в XXI веке могла соответствовать надпись, в предположении, что одно из чисел соответствует дню в месяце (дни в каждом месяце нумеровались с единицы), еще одно из чисел — номеру месяца (месяцы также нумеровались с единицы), и еще одно число — последним двум цифрам года в XXI веке григорианского календаря.

По заданной надписи на диске выясните, каким датам в XXI веке она могла соответствовать.

Во входном файле в формате `"aa"//"bb"//"cc"` записаны числа с диска.

В выходной файл в произвольном порядке выведите все корректные даты `"dd"//"mm"//"yy"` в XXI веке, где `"dd"` соответствует номеру дня, `"mm"` -- номеру месяца, `"yy"` — номеру года, причем числа, соответствующие `"dd"`, `"mm"` и `"yy"` являются перестановками чисел с диска.

В случае, если никакая перестановка исходных чисел не является корректной датой XXI века, выведите "No such date".

29/02/04

29/02/04
29/04/02
02/04/29
04/02/29

01/01/01

01/01/01

99/99/99

No such date

В Берляндии наступила эпоха просвещения. Уставшие от длительного средневековья, постоянных войн, драконов, принцесс, рыцарей, спасающих принцесс от драконов, и прочего героизма жители Берляндии обратились к прекрасному — к икебане. На этот год назначено проведение грандиозного соревнования среди любителей икебаны, однако в связи с недавно закончившимся средневековьем жюри испытывает массу проблем. В частности, в Берляндии из растений, пригодных для составления икебаны, остался только волшебный бамбук.

После долгих прений жюри утвердило регламент проведения соревнований. Соревнования длятся `m` дней. Всем участникам выдаются одинаковые грядки с `n` ростками бамбука. В момент начала соревнований — 5:00 первого дня — высота `i`-го ростка на грядке каждого участника равна `a_i`. Каждую полночь `i`-й росток вырастает на `b_i`. Утром каждого дня, начиная с первого, ровно в 6:00, каждый участник может один раз постричь бамбук на своей грядке. Происходит это так: участник выбирает `i` и `j` (`1\ ≤\ i\ ≤\ j\ ≤\ n`) — левую и правую границу отрезка ростков, которые он хочет постричь, затем выбирает высоту `l` (`0\ ≤\ l\ ≤\ 2*10^9`), и все ростки, с `i`-го по `j`-й включительно, высота которых больше `l`, обрезаются до высоты `l`. Сравнение работ происходит в полдень `m`-го дня. Победителями соревнований считаются те участники, которые, сделав минимальное количество стрижек, смогли получить грядку, все `n` ростков на которой имеют высоту `h`.

Теперь жюри интересно, какое минимальное число раз победителю придется стричь бамбук.

В первой строке входного файла находится три целых числа: `n` (`1\ ≤\ n\ ≤\ 10^5`) — количество ростков бамбука на грядке, `m` (`1\ ≤\ m\ ≤\ 10^9`) — длительность соревнований, и `h` (`0\ ≤\ h\ ≤\ 10^9`) — высота всех ростков, необходимая для победы.

В следующих `n` строках находится по два целых числа `a_i` и `b_i` `(0\ ≤\ a_i,\ b_i\ ≤\ 10^9)` — описание `i`-го ростка: его высота в момент начала соревнований и на сколько он вырастает за ночь, сооветственно.

В выходной файл выведите одно число — минимальное число стрижек бамбука, необходимое, чтобы весь бамбук в конце соревнования имел высоту `h`, либо число `-1`, если это невозможно.

1 1 3
2 1

-1

2 2 3
20 1
10 1

1

В первом примере подведение итогов происходит в тот же день, что и начало соревнований. Для победы необходимо иметь росток бамбука высотой 3, но бамбук растет в полночь, и между 5 утра и полуднем высота бамбука не изменится и останется равной 2. При этом стрижка бамбука позволяет лишь уменьшить его высоту, поэтому достичь цели невозможно.

Во втором примере можно, например, подстричь все ростки бамбука в первый день до высоты 2, ночью все ростки бамбука вырастут на 1 и будут иметь искомую высоту к полудню второго дня.

Однажды робот-библиотекарь решил устроить ревизию. На одной из полок, среди экземпляров тридцать третьего издания Кормена, он нашел листок из условий одного древнего контеста. Роботу известен формат оформления условий, однако этот листок привел его в замешательство.

Обычно внизу каждой страницы условий есть надпись вида "Страница `i` из `n`", где `i` — номер страницы условий, а `n` — количество страниц в условиях. Однако на этом листе была всего одна длинная последовательность цифр. Видимо, принтер почему-то не напечатал ни одного символа кроме цифр. Таким образом, номера `i` и `n` слились в единую последовательность цифр.

Теперь понять, какой же был номер у найденной страницы, стало большой проблемой, и решений у этой задачи может быть много. Роботу стало интересно, сколько существует решений, но так как робот не предназначен для решения таких задач, он нуждается в вашей помощи. Страницы в условиях нумеруются от 1 до `n`, числа `i` и `n` записываются без ведущих нулей.

Выясните, сколько есть корректных надписей вида "Страница `i` из `n`", при удалении из которых всех символов кроме цифр получается заданная во входном файле строка.

Входной файл содержит строку, состоящую только из цифр. Длина строки лежит в пределах от 1 до `200\ 000`, включительно.

Выведите количество корректных надписей вида "Страница `i` из `n`", при удалении из которых всех символов кроме цифр получается заданная во входном файле строка.

23507645

3

Многим из вас, наверное, известна легенда про Ханойскую башню. Легенда гласит, что в одном далеком монастыре находится бронзовый диск, на котором закреплены три алмазных стержня. Давным-давно, в самом начале времен, монахи этого монастыря провинились перед богами. Разгневанные боги положили `n` дисков на один из стержней, все диски имели разные радиусы и были расположены по убыванию радиуса — самый большой диск лежал снизу, на нем диск поменьше, … , самый маленький диск располагался сверху. Монахи должны перекладывать диски между стержнями, причем каждый раз должны класть диск либо на пустой стержень, либо поверх большего диска. Как только все `n` дисков будут переложены со стержня, на который боги сложили их, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир.

Однако недавно Петя прочитал новую версию легенды. Согласно этой легенде, в Пизанской башне есть аналогичная головоломка, но второй стержень у нее наклонен. Со второго стержня можно снимать сразу несколько дисков, лежащих сверху, и перекладывать их вместе, не меняя порядка, на другой стержень. При этом группу дисков также можно перекладывать либо на пустой стержень, либо на диск, который больше нижнего из перекладываемых дисков.

По легенде, когда все диски будут перенесены с первого стержня на третий, Пизанская башня перестанет наклоняться и начнет стоять ровно.

Петю заинтересовало, за какое минимальное число действий можно перенести все диски с первого стержня Пизанской головоломки на третий. Помогите ему выяснить это.

Во входном файле задано единственное натуральное число `n` (`1\ ≤\ n\ ≤\ 40`) — количество дисков.

Выведите единственное число — минимальное число перекладываний, необходимое для того, чтобы все диски оказались на третьем стержне.

3

5

В примере можно действовать следующим образом: переложить маленький диск с первого стержня на третий, затем средний диск с первого на второй, затем маленький с третьего на второй (поверх среднего), затем большой диск с первого на третий, и, наконец, последним действием пару дисков со второго стержня на третий. Всего необходимо пять действий.

Первокурсник Макс только что решил с головой погрузиться в учебу. К завтрашнему семинару по мифологии ему необходимо подготовить доклад в `k` страниц. Макс любит мифологию, так что доклад уже готов, осталось только его распечатать.

К сожалению, во всех имеющихся в общежитии принтерах закончились картриджи, и теперь Максу придется купить новые картриджи для печати доклада. В магазине обнаружилось `n` типов картриджей. Продавец объяснил Максу, что картридж имеет два основных параметра — стоимость и количество страниц, на печать которых его хватает.

Выяснилось, что картридж `i`-го типа стоит `c_i` рублей и может напечатать `p_i` страниц. В магазине есть в наличии неограниченное количество картриджей каждого типа.

Макс — бедный студент, поэтому он хочет как можно дешевле приобрести картриджи, которых вместе бы хватило для печати доклада. С другой стороны, Макс очень жадный. Он знает, что если после печати доклада у него останется ресурс хотя бы на одну страницу, еще год все в общежитии будут ходить к нему распечатывать документы.

Поэтому Макс хочет купить картриджей с минимальной суммарной стоимостью, которых достаточно для печати ровно `k` страниц.

Помогите Максу — посчитайте минимальную сумму, на которую ему придется раскошелиться.

В первой строке входного файла содержатся числа `n` — количество типов картриджей в ассортименте магазина и `k` — количество страниц в докладе Макса (`1\ ≤\ n\ ≤\ 100\ 000`, `1\ ≤\ k\ ≤\ 10^{9}`). Далее следуют `n` строк, `i`-я из них содержит числа `c_i` и `p_i` (`1\ ≤\ c_i,\ p_i\ ≤\ 200`) — стоимость картриджа `i`-го типа и число страниц, которое можно распечатать с его помощью, соответственно.

Выходной файл должен содержать одно число — минимальное количество денег, которое придется потратить Максу, чтобы распечатать ровно `k` страниц. Если решения не существует, выведите в выходной файл `-1`.

4 5
5 5
2 3
5 10
1 1

4

1 2
1 3

-1

В первом примере Максу следует купить один картридж второго типа и два картриджа четвертого типа. Заплатив 4 рубля, Макс получит возможность напечатать ровно 5 страниц.

Во втором примере есть лишь один тип картриджей, купив его, Макс получит возможность напечатать 3 страницы, что больше требуемых двух.

Одной из проблем, которые приходится решать любому программисту, является нехватка памяти, которую может использовать программа. Часто, чтобы уменьшить объем используемой программой памяти, программисты используют различные структуры данных, одной из которых и является квадродерево.

Опишем суть этой структуры данных. Квадродерево позволяет нам представлять в памяти таблицу размера `2^n\ times\ 2^n`, состоящую из нулей и единиц. Все дерево состоит из ячеек, каждая ячейка отвечает за некоторую часть этой таблицы, при этом каждая часть является квадратом со стороной `2^p`. Первая ячейка отвечает за всю таблицу.

Если все элементы квадрата, за который отвечает ячейка, имеют одинаковое значение (`0` или `1`), то в ячейке просто хранится эта информация. Если же внутри квадрата существуют хотя бы два различных элемента, то весь квадрат делится на четыре непересекающихся квадрата со стороной `2^{p\ -\ 1}`, после чего для каждой четверти создается отдельная ячейка, и ссылки на все четыре созданных ячейки записываются в ячейку, отвечающую за большой квадрат.

Правильное квадродерево для данной таблицы. Любой квадрат, у которого все четыре стороны выделены, является ячейкой квадродерева. Всего используется 13 ячеек.

Далеко не всегда подобный способ хранения таблицы приводит к сокращению объема памяти. Но не во всех задачах требуется абсолютно точно хранить всю таблицу, не потеряв значения ни одного элемента. Иногда можно потерять часть информации. А именно, разрешается изменить значения не больше, чем `k` элементов таблицы.

Выясните, какое минимальное возможное количество ячеек может быть в квадродереве, описывающем таблицу, получающуюся из данной изменением не более, чем `k` элементов.

Первая строка входного файла содержит два целых числа `t=2^n` и `k` — размер таблицы и максимальное количество измененных ячеек соответственно (`2\ ≤\ t\ ≤\ 128`, `1\ ≤\ k\ ≤\ t^2`).

Гарантируется, что `t` является степенью двойки.

Следующие `t` строк содержат по `t` символов, каждый из которых является `0` или `1`. Эти строки описывают заданную таблицу.

Выведите в выходной файл одно целое число — минимальное возможное количество ячеек в квадродереве, описывающем таблицу, получающуюся из данной изменением не более, чем `k` элементов.

4 2
0001
0010
0000
0010

9

В приведенном примере можно, например, заменить две верхних единицы на нули. После этого получается таблица

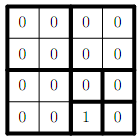
Для ее хранения с помощью квадродерева необходимо 9 ячеек: одна для всей таблицы, четыре для четырех квадратов `2\ times\ 2`, три из них содержат 0, а четвертый, соответствующий нижнему правому углу, разбивается еще на четыре.

Археологический раздел НИИЧАВО решил заняться изучением древнефлатландских волшебных шпаг. После изучения всех имеющихся в наличии образцов было выяснено, что почти все шпаги на самом деле являются копиями друг друга.

А именно, в глубокой древности была произведена первая волшебная шпага. Время от времени мастера брали одну из существующих волшебных шпаг и изготавливали ее копию. Разумеется, копия отличалась от оригинала, но в целом наследовала некоторые его признаки.

Поскольку изготовление копии волшебной шпаги снижает ее магическую силу, ученые установили, что с каждой шпаги было сделано не более двух копий. Также было установлено, что копия могла быть изготовлена не ранее чем через `k` лет после изготовления оригинала.

В распоряжении ученых оказались `n` шпаг, про каждую из которых им известен ее возраст. Ученые хотят выяснить, какая из шпаг была изготовлена первой, а для всех остальных шпаг выяснить, с какой из шпаг она была скопирована. К сожалению, информации о возрасте может быть недостаточно, чтобы восстановить эту информацию однозначно, но ученых устроит любой возможный вариант.

Первая строка входного файла содержит два числа `n` и `k` — количество шпаг, имеющихся у ученых, и минимальный возраст, необходимый для того, чтобы со шпаги можно было сделать копию (`1\ ≤\ n\ ≤\ 100\ 000`, `1\ ≤\ k\ ≤\ 10^8`). Следующая строка содержит `n` чисел: `a_1,\ a_2,\ …,\ a_n`, где `a_i` (`0\ ≤\ a_i\ ≤\ 10^{9}`) — возраст `i`-й шпаги.

Для каждого экземпляра шпаги выведите номер шпаги, с которой она была скопирована. Обратите внимание, с каждой шпаги могло быть снято не более двух копий.

Если экземпляр является первой изготовленной шпагой, то выведите для соответствующей шпаги число 0.

Если возможных решений несколько, выведите любое.

Если ученые ошибаются, и не существует последовательности, в которой копии шпаг могли бы быть изготовлены, выведите единственное число `-1`.

6 3
2 10 6 0 5 2

5 0 2 3 2 5

4 3
10 1 1 1

-1

Всем известно, что в городах есть большая проблема — пробки. Пробка образуется, когда по дороге пытаются ехать сразу много машин. При этом основная причина образования пробок — перекрестки. Самые большие пробки образуются именно на них.

В одном городе на перекрестке, на котором пересекаются две односторонние дороги, решили установить светофор.

В каждый момент светофор либо горит зеленым для машин на первой дороге, либо горит зеленым для машин на второй дороге, либо переключается между этими режимами. По правилам дорожного движения, в моменты переключения светофора можно ехать по любой дороге.

Светофор устроен следующим образом. В момент времени `0` он загорается зеленым для машин на первой дороге и красным для машин на второй дороге. Далее, через `g` секунд он переключается на красный для машин на первой дороге и зеленый для машин на второй дороге, после чего через `r` секунд переключается обратно на зеленый для первой дороги, и т. д.

Таким образом, светофор горит зеленым для первой дороги в моменты времени `(\ k(r\ +\ g),\ k(r\ +\ g)\ +\ g)` для целых `k` и зеленым для второй дороги — в `(\ k(r\ +\ g)\ +\ g,\ (k\ +\ 1)(r\ +\ g)\ )`. Переключения же происходят в моменты `k(r\ +\ g)` и `k(r\ +\ g)\ +\ g`. Когда светофор горит зеленым для первой дороги, по ней могут ехать машины, а по второй — нет, и наоборот. Будем считать что в момент переключения, могут проезжать машины с обеих дорог. Считается что машина проехала в момент переключения, если момент, когда она проехала, и момент переключения отличаются не более чем на `10^{-5}`.

В соответствии с технической документацией период работы светофора зафиксирован и должен быть равен `x`, иначе говоря, должно выполняться равенство `r\ +\ g\ =\ x`. С соблюдением этого условия значения `r` и `g` можно выбрать любыми неотрицательными вещественными числами.

Для выбора оптимальных значений `r` и `g` было проведено исследование трафика на дорогах и получены следующие данные.

На каждой из дорог находится несколько машин, которые едут в сторону перекрестка. Машины не обгоняют друг друга. Каждый раз, когда машина догоняет более медленную, она снижает скорость и следует непосредственно за ней с соответствующей скоростью. Размерами машин и временем на изменение скорости можно пренебречь. Когда машина подъезжает к перекрестку, если горит зеленый свет или происходит переключение, то она немедленно проезжает перекресток. В противном случае машина останавливается и ждет включения зеленого света.

В момент 0 на первой дороге расположены `n` машин, `i`-я из них находится на расстоянии `a_i` метров от перекрестка и движется в его сторону со скоростью `v_i` м/с.

Аналогично, на второй дороге расположены `m` машин, `i`-я из них находится на расстоянии `b_i` метров от перекрестка и движется в его сторону со скоростью `w_i` м/с.

Чтобы пробок в городе было меньше, необходимо выбрать такие `g` и `r`, чтобы максимальное число машин, которые одновременно стоят на перекрестке, было как можно меньше.

Помогите управлению дорожного движения выбрать оптимальные `g` и `r`.

В первой строке задано вещественное число `x` (`1\ ≤\ x\ ≤\ 10^4`), с не более чем тремя знаками после десятичной точки. Во второй строке задано число `n` (`0\ ≤\ n\ ≤\ 100\ 000`) — количество машин на первой дороге. Далее, в `n` строках задано описание машин на первой дороге. Описание каждой машины состоит из двух вещественных чисел `a_i` и `v_i` — расстояния от машины до перекрестка и ее скорости, соответственно (`1\ ≤\ a_i,\ v_i\ ≤\ 10^4`). Числа `a_i` и `v_i` заданы не более, чем с тремя знаками после десятичной точки.

В следующей строке задано число `m` (`0\ ≤\ m\ ≤\ 100\ 000`, `1\ ≤\ n\ +\ m\ ≤\ 100\ 000`) — количество машин на второй дороге. Далее, в `m` строках задано описание машин на второй дороге. Описание каждой машины состоит из двух вещественных чисел `b_i` и `w_i` — расстояния от машины до перекрестка и ее скорости, соответственно (`1\ ≤\ b_i,\ w_i\ ≤\ 10^4`). Числа `b_i` и `w_i` заданы не более, чем с тремя знаками после десятичной точки.

Никакие две машины исходно не находятся в одной точке. Оба списка машин даны в порядке возрастания расстояния до светофора.

На первой строке выходного файла выведите минимальное `k`, такое что выбором `g` и `r` можно добиться, чтобы на перекрестке никогда не стояло одновременно более `k` машин.

На второй строке выведите два вещественных числа `g` и `r`, позволяющие добиться искомого. Следует выводить `g` и `r` не менее чем с 6 знаками после десятичной точки.

Если существует несколько оптимальных решений, выведите любое.

2.0
1 
1.0 1.0
2
1.0 1.0
2.0 2.0

0
1.00000 1.00000

4.0
3 
2.0 1.0
4.0 5.0
5.0 20.0
3
1.0 1.0
5.0 1.0
7.0 1.0

1
2.00000 2.00000

В первом примере все машины подъезжают к перекрестку в момент 1. Сделав переключение светофора как раз в этот момент можно обеспечить проезд всех машин без ожидания.

Во втором примере на первой дороге ситуация развивается следующим образом. Сначала через `1/15` секунды третья машина догоняет вторую и ей приходится снизить скорость до 5 м/с. Затем они вместе догоняют первую машину в момент 0.5, им обеим приходится снизить скорость до 1 м/с. Так вместе они и подъезжают к перекрестку через 2 секунды после начала движения.

На второй дороге машины движутся с равной скоростью и подъезжают к перекрестку через 1, 5 и 7 секунд после начала движения, соответственно. При любом выборе `g` и `r` хотя бы одной машине придется ждать. Оптимально выбрать любое значение `g` от 2 до 3, включительно. В этом случае ждать будут первая и вторая машины на второй дороге, но одновременно на перекрестке будет находиться не более одной машины. Если выбрать `g\ <\ 2`, то придется ждать трем машинам на первой дороге, а если выбрать `g\ >\ 3`, то вторая и третья машины на второй дороге будут одновременно ждать на перекрестке.

Ваня, Сережа и Дима любят физические нагрузки. Больше всего им нравится поднимать тяжести. Ребята очень давно начали заниматься гиревым спортом и уже собрали набор гирь для тренировок. Этот набор состоит из `n` гирь с различными целыми весами от 1 до `n`.

Совсем недавно ребята нашли новый спортивный зал и решили перенести туда все свои гири. Так как им очень нравится их поднимать, то каждому хочется нести как можно больший вес. Но ребята очень честные, и весь вес решили распределить поровну. Помогите спортсменам разделить набор из `n` гирь с весами `1,\ 2,\ …,\ n` на три равные по весу части.

Входной файл содержит единственное целое число `n` (`1\ ≤\ n\ ≤\ 100\ 000`) — количество гирь.

Выведите для каждого спортсмена набор гирь, который ему нужно перенести в новый спортивный зал. Наборы выводятся следующим образом. В первой строке выведите количество гирь в наборе. Далее, во второй строке через пробел выведите веса гирь.

Если разбить все гири на три равных по весу множества нельзя, выведите "Impossible".

Если существует несколько решений, можно вывести любое.

6

2
3 4
2
5 2
2
1 6

3

Impossible