Начало
Соревнования
Задачи 2 тура областной олимпиады по информатике 2011
5. Шахматная доска
Вывод формулыОлимпиадные задачи на русском языке
| 23/01/2011 | Областная олимпиада школьников по информатике. II тур. (5) |
| 12/07/2019 | Лето 2019 - 6 (командное) (C) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
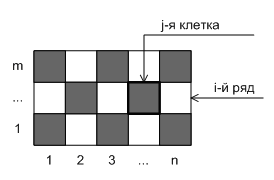
Аня разделила доску размера `m\ times\ n` на клетки размера
`1\ times\ 1` и раскрасила их в черный и белый цвет в шахматном порядке.
Васю заинтересовал вопрос: клеток какого цвета получилось больше — черного
или белого.
Для того, чтобы выяснить это, он спросил у Ани, в какой цвет она
раскрасила `j`-ю клетку в `i`-м ряду доски.
По этой информации Вася попытался определить,
клеток какого цвета на доске больше.
Требуется написать программу, которая по размерам доски и цвету j-й клетки в i-м ряду определит, клеток какого цвета на доске больше — черного или белого.
Формат входного файла
Входной файл содержит пять целых чисел: `m`, `n`, `i`, `j` и `c`
(`1\ ≤\ m,\ n\ ≤\ 10^9`, `1\ ≤\ i\ ≤\ m`, `1\ ≤\ j\ ≤\ n`, `с\ =\ 0` или `с\ =\ 1`).
Значение `c\ =\ 0` означает, что `j`-я клетка в `i`-м ряду доски раскрашена в
черный цвет, а значение `c\ =\ 1` — в белый цвет.
Формат выходного файла
Выходной файл должен содержать одно из трех слов:
- black, если черных клеток на доске больше,
- white, если белых клеток на доске больше,
- equal, если черных и белых клеток на доске поровну.
Пример ввода 1
3 5 1 1 0
Пример вывода 1
black
Пример ввода 2
3 5 2 1 0
Пример вывода 2
white
Пример ввода 3
4 4 1 1 1
Пример вывода 3
equal
Примечание
Правильные решения для тестов, в которых `1\ ≤\ m,\ n\ ≤\ 100`, оцениваются из 50 баллов.
Источник: региональный этап Всероссийской олимпиады по информатике 2010/2011, http://neerc.ifmo.ru/school/ 6. Чемпионат по стрельбе
Полный переборОлимпиадные задачи на русском языке
| 23/01/2011 | Областная олимпиада школьников по информатике. II тур. (6) |
| 25/06/2012 | 1 курс, дорешивание (6G2) |
| 02/07/2012 | 1 курс, день 6, группа 2 (G2) |
Ограничения: время – 2s/5s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
Победитель школьного этапа олимпиады по информатике нашел дома в
старых бумагах результаты чемпионата страны по стрельбе из лука,
в котором участвовал его папа. К сожалению, листок с результатами
сильно пострадал от времени, и разобрать фамилии участников
было невозможно. Остались только набранные каждым участником
очки, причем расположились они в том порядке, в котором
участники чемпионата выполняли стрельбу.
Расспросив папу, школьник выяснил, что количество очков, которое набрал
папа, заканчивается на 5, один из победителей чемпионата стрелял раньше,
а папин друг, который стрелял сразу после папы, набрал меньше очков.
Теперь он заинтересовался, какое самое высокое место мог
занять его папа на том чемпионате.
Будем считать, что участник соревнования занял `k`-е место, если ровно
`(k\ –\ 1)` участников чемпионата набрали строго больше очков, чем он.
При этом победителями считались все участники чемпионата,
занявшие первое место.
Требуется написать программу, которая по заданным результатам
чемпионата определяет, какое самое высокое место на
чемпионате мог занять папа победителя школьного этапа олимпиады по информатике.
Формат входного файла
Первая строка входного файла содержит целое число `n` — количество
участников чемпионата страны по стрельбе (`3\ ≤\ n\ ≤\ 10^5`).
Вторая строка входного файла содержит `n` положительных целых чисел,
каждое из которых не превышает 1000, — очки участников чемпионата,
приведенные в том порядке, в котором они выполняли стрельбу.
Формат выходного файла
В выходном файле должно содержаться одно целое число — самое высокое место,
которое мог занять папа школьника. Если не существует
ни одного участника чемпионата, который удовлетворяет,
описанным выше условиям, выведите в выходной файл число 0.
Пример ввода 1
7 10 20 15 10 30 5 1
Пример вывода 1
6
Пример ввода 2
3 15 15 10
Пример вывода 2
1
Пример ввода 3
3 10 15 20
Пример вывода 3
0
Примечание
Правильные решения для тестов, в которых `1\ ≤\ n\ ≤\ 1000`, оцениваются из 50 баллов.
Источник: региональный этап Всероссийской олимпиады по информатике 2010/2011, http://neerc.ifmo.ru/school/ 7. Делители
Рекурсивный переборСокращение перебора с помощью идеи
Олимпиадные задачи на русском языке
| 23/01/2011 | Областная олимпиада школьников по информатике. II тур. (7) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
Натуральное число `a` называется делителем натурального числа `b`, если `b\ =\ "ac"`
для некоторого натурального числа `c`. Например, делителями
числа 6 являются числа 1, 2, 3 и 6. Два числа называются взаимно
простыми, если у них нет общих делителей кроме 1. Например, 16 и 27 взаимно
просты, а 18 и 24 — нет.
Будем называть нормальным набор из `k` чисел (`a_1,\ a_2,\ …,\ a_k`),
если выполнены следующие условия:
- каждое из чисел `a_i` является делителем числа `n`;
- выполняется неравенство `a_1\ <\ a_2\ <\ …\ <\ a_k`;
- числа `a_i` и `a_{i+1}` для всех `i` от 1 до `k\ –\ 1` являются взаимно простыми;
- произведение `a_1*a_2*…*a_k` не превышает `n`.
Например, набор (2, 9, 10) является нормальным набором из 3 делителей
числа 360.
Требуется написать программу, которая по заданным значениям `n` и `k` определяет
количество нормальных наборов из `k` делителей числа `n`.
Формат входного файла
Первая строка входного файла содержит два целых числа: `n` и `k` (`2\ ≤\ n\ ≤\ 10^8`,
`2\ ≤\ k\ ≤\ 10`).
Формат выходного файла
В выходном файле должно содержаться одно число — количество нормальных наборов из `k` делителей числа `n`.
Пример ввода 1
90 3
Пример вывода 1
16
Пример ввода 2
10 2
Пример вывода 2
4
Примечание
Правильные решения для тестов, в которых `n\ ≤\ 1000` и `k\ =\ 2`, оцениваются
из 30 баллов.
Правильные решения для тестов, в которых `k\ =\ 2`, оцениваются из 60 баллов
(в эти баллы включаются также 30 баллов для случая `n\ ≤\ 1000`, `k\ =\ 2`).
Источник: региональный этап Всероссийской олимпиады по информатике 2010/2011, http://neerc.ifmo.ru/school/ 8. Дом у дороги
ГеометрияОлимпиадные задачи на русском языке
| 23/01/2011 | Областная олимпиада школьников по информатике. II тур. (8) |
Ограничения: время – 2s/4s, память – 256MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
Министерство дорожного транспорта решило построить себе новый офис.
Поскольку министр регулярно выезжает с инспекцией наиболее важных трасс,
было решено, что офис министерства не должен располагаться
слишком далеко от них.
Наиболее важные трассы представляют собой прямые на плоскости.
Министерство хочет выбрать такое расположение для своего офиса,
чтобы максимум из расстояний от офиса до трасс был как можно меньше.
Требуется написать программу, которая по заданному расположению
наиболее важных трасс определяет оптимальное расположение дома
для офиса министерства дорожного транспорта.
Формат входного файла
Первая строка входного файла содержит одно целое число `n` — количество
наиболее важных трасс (`1\ ≤\ n\ ≤\ 10^4`).
Последующие `n` строк описывают трассы. Каждая трасса описывается
четырьмя целыми числами `x_1`, `y_1`, `x_2` и `y_2` и представляет
собой прямую, проходящую через точки `(x_1,\ y_1)` и `(x_2,\ y_2)`.
Координаты заданных точек не превышают по модулю `10^4`.
Точки `(x_1,\ y_1)` и `(x_2,\ y_2)` ни для какой прямой не совпадают.
Формат выходного файла
Выходной файл должен содержать два разделенных пробелом
вещественных числа: координаты точки, в которой следует построить
офис министерства дорожного транспорта. Координаты по модулю
не должны превышать `10^9`, гарантируется, что хотя бы один
такой ответ существует. Если оптимальных ответов несколько,
необходимо выведите любой из них.
Ответ должен иметь абсолютную или относительную погрешность не более `10^{-6}`,
что означает следующее. Пусть максимальное расстояние
от выведенной точки до некоторой трассы равно `x`, а в правильном
ответе оно равно `y`. Ответ будет засчитан, если значение
выражения `|x\ –\ y|\ /\ max{1,\ |y|\ }` не превышает `10^{-6}`.
Пример ввода
4 0 0 0 1 0 0 1 0 1 1 2 1 1 1 1 2
Пример вывода
0.5 0.5
Примечание
Правильные решения для тестов, в которых `n\ ≤\ 100` и все прямые параллельны,
оцениваются из 20 баллов.
Правильные решения для тестов, в которых `n\ ≤\ 100` и все прямые параллельны
осям координат, оцениваются из 20 баллов.
Правильные решения для тестов, в которых `n\ ≤\ 100`, оцениваются из 70 баллов
(в эти баллы включаются также по 20 баллов за случаи, описанные в предыдущих двух абзацах).
Источник: региональный этап Всероссийской олимпиады по информатике 2010/2011, http://neerc.ifmo.ru/school/ 