Разбор задачи

Задачу можно представить как ориентированный граф, в котором вершины соответствуют числам от 0 до `2^n-1`. Дуги соединяют числа, которые могут следовать друг за другом в числе Уробороса.

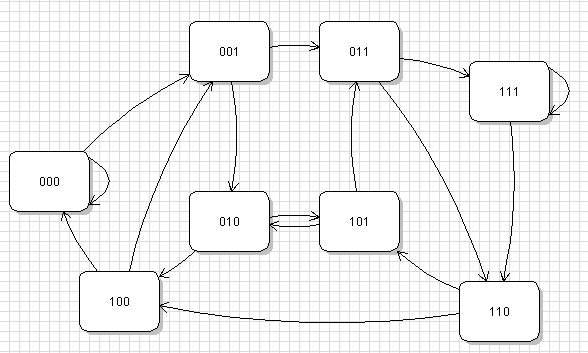
В этом графе нужно построить замкнутый путь, проходящий по всем вершинам графа только один раз. Это известная задача о построении Гамильтонова цикла, которая в общем случае является NP-полной, т.е. время решения будет расти экспоненциально от числа вершин. Хотя на данном графе хорошо работает рекурсивный перебор, так как возврат при переборе необходим достаточно редко, и для n=21 на построение Гамильтонова цикла требуется около 1 секунды. Но для организации рекурсии требуется либо большой стек, поддерживаемый не во всех компиляторах, либо довольно сложный код. Лучше построить другой граф, в котором вершинами служат числа от 0 до `2^{n-1}-1` бит, а дуги пронумерованы числами от 0 до `2^n-1`. Дуга с номером `x` соединяет вершины с номерами `[x/2]`, т.е. `(n-1)` старших бит номера дуги, и `x\ mod\ 2^{n-1}`, т.е. `(n-1)` младших бит номера дуги.

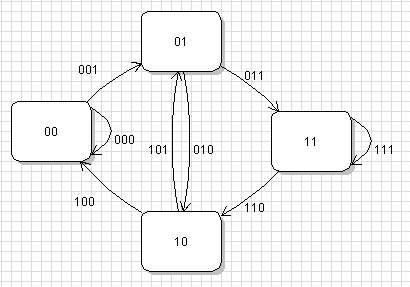
В этом случае задача сводится к построению Эйлерова цикла, что выполняется за время `O(2^n)`. Минимальное число Уробороса можно получить, если начать путь с дуги 00..0.