Разбор задачи J. Пластинки

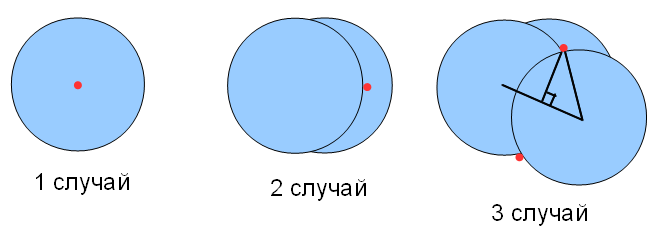
• Одиночная пластинка или несколько пластинок стопкой. Нужно проверить центр круга `(X_i,Y_i)`. Количество точек такого типа равно `N`.
  
• Одна пластинка накладывается на другую, при этом центр другой пластинки невидим. Нужно проверить точку, которая находится на расстоянии `R+ε` от центра первой пластинки по направлению к центру другой пластинки. Для нахождения координат точки нужно "масштабировать" вектор, соединяющий центры кругов – привести его к единичному, поделив обе координаты вектора на его длину, затем умножить координаты на новую длину. Координаты точки будут равны `(X_i+(X_j-X_i)*(R+ε)/D_{ij},\ Y_i+(Y_j-Y_i)*(R+ε)/D_{ij})`, где `j<i`, `D_{ij}` – расстояние между центрами пластинок `i` и `j`, `0\ <\ D_{ij}\ ≤\ R`, `ε=10^{-6}`. Количество точек такого типа не превышает `N*(N-1)/2`.
  
• Пластинку накрывает две или больше пластинок. Видимая часть накрытой пластинки представляет собой "многоугольник", образованный дугами краев накрывающих пластинок и, возможно, края самой пластинки. Нужно проверить 2 точки, лежащие на расстоянии `ε` от двух точек пересечения краев накрывающих пластинок. Для нахождения координат точек выполняем поворот на `90°` и `-90°` и масштабирование вектора, соединяющий центры кругов. Расстояние `P` от точек пересечения до середины отрезка, соединяющего центры кругов, равно `sqrt(R^2\ -\ D_{ij}^2/4)`. Середина отрезка между центрами кругов имеет координаты `((X_j+X_i)/2,\ (Y_j+Y_i)/2)`. Координаты точек равны `((X_j+X_i)/2\ -\ (Y_j-Y_i)*(P+ε)/D_{ij},\ (Y_j+Y_i)/2\ +\ (X_j-X_i)*(P+ε)/D_{ij})` и `((X_j+X_i)/2\ +\ (Y_j-Y_i)*(P+ε)/D_{ij},\ (Y_j+Y_i)/2\ -\ (X_j-X_i)*(P+ε)/D_{ij})`, где `j<i`, `0\ <\ D_{ij}\ ≤\ 2*R`, `ε=10^{-6}`. Количество точек такого типа не превышает `N*(N-1)`.