Начало
Соревнования
Разбор задачи E. Сигнальная система
Тема: вычислительная геометрия, кратчайший путь между парами вершинСложность: выше среднего
Нужно отметить, что некоторые ограничения, получающиеся из реалистичности задачи, можно не учитывать в программе, так как требование минимизации количества отражений автоматически приводит к их выполнению.
Если луч дважды проходит через одно зеркало с отражением или без него, следовательно, путь луча можно сократить.
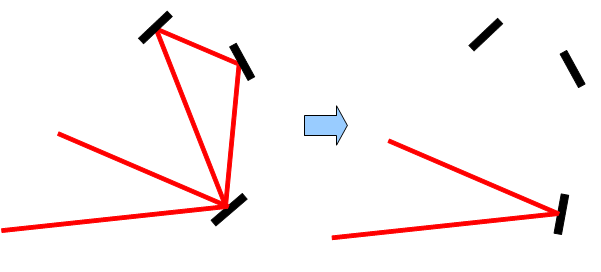и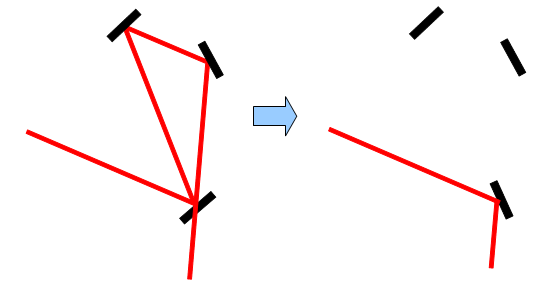 
Если угол между падающим на зеркало лучом и отраженным равен 180 градусов, то такое зеркало можно просто убрать.
Для проверки пересечения луча с препятствиями можно воспользоваться либо общим алгоритмом, описанным в книге Кормена и др. "Алгоритмы: построение и анализ", либо написать самостоятельно алгоритм для пересечения с горизонтальным или вертикальным отрезком, который необходим в этой задаче. Рассмотрим только случай пересечения с вертикальным отрезком, так как для горизонтального отрезка нужно только поменять местами значения ординат и абсцисс при вызове функции. Перед рассмотрением вариантов необходимо обменять точки так, чтобы `x_1\ ≤\ x_2` и `y_3\ ≤\ y_4`.
Возможны следующие случаи:
- Отрезок `(x,y_3)-(x,y_4)` находится за пределами полосы, где находится отрезок `(x_1,y_1)-(x_2,y_2)`, т.е. `x\ <\ x_1` или `x\ >\ x_2`. Отрезки не пересекаются.
- Отрезок `(x_1,y_1)-(x_2,y_2)` также является вертикальным, т.е. `x_1\ =\ x_2\ =\ x`. Тогда отрезки пересекаются, если `y_4\ ≥\ y_1` и `y_3\ ≤\ y_2`.
- Отрезок `(x,y_3)-(x,y_4)` находится в полосе, где находится отрезок `(x_1,y_1)-(x_2,y_2)`. Используя подобие треугольников, найдем на отрезке `(x_1,y_1)-(x_2,y_2)` точку с абсциссой `x`: `y\ =\ y_1\ +\ {(y_2-y_1)*(x-x_1)}/{x_2-x_1}`. Отрезки пересекаются, если `y_3\ ≤\ y` и `y\ ≤\ y_4`. Чтобы избавиться от погрешностей вычислений, можно домножить все ординаты на `x_2-x_1` и проверять условие `y_3*(x_2-x_1)\ ≤\ y_1*(x_2-x_1)\ +\ (y_2-y_1)*(x-x_1)\ ≤\ y_4*(x_2-x_1)`.
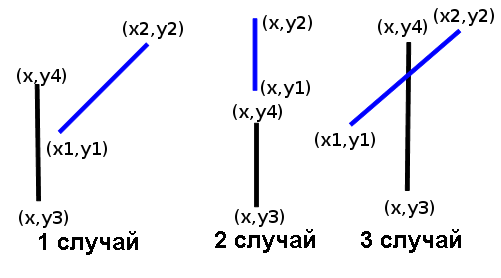
procedure swap(var a,b:longint);
var t:longint;
begin
t:=a;
a:=b;
b:=t;
end;
function iscross(x1,y1,x2,y2,x,y3,y4:longint):boolean;
var y:longint;
begin
if x1>x2 then
begin
swap(x1,x2);
swap(y1,y2);
end;
if y3>y4 then
swap(y3,y4);
if (x<x1) or (x>x2) then
begin { 1 случай }
iscross:=false;
exit;
end;
if x1=x2 then
begin { 2 случай }
if y1>y2 then
swap(y1,y2);
iscross:=(y4>=y1) and (y3<=y2);
exit;
end;
{ 3 случай }
y:=y1*(x2-x1)+(y2-y1)*(x-x1);
iscross:=(y3*(x2-x1)<=y) and (y<=y4*(x2-x1));
end;
Чтобы найти путь луча с минимальным количеством отражений (использованных зеркал), а среди них с минимальный длиной пути, можно искать кратчайший путь в графе, где длина ребра равна расстоянию между точками плюс `10^6`. Так число вершин в таком графе равно `N+2\ ≤\ 102` (`N` точек для установки зеркал, а также источник и приемник), то для поиска кратчайшего пути между источником и приемником можно использовать алгоритм Флойда-Уоршалла.
const inf:extended=1e100;
var dist:array[1..102,1..102] of extended;
can:array[1..102,1..102] of boolean;
...
{ составление матрицы с расстояниями }
for i:=1 to n2 do
begin
for j:=i to n2 do
begin
can[i,j]:=canlight(i,j);
if can[i,j] then
dist[i,j]:=1e6+sqrt(sqr(point[i].x-point[j].x)+sqr(point[i].y-point[j].y))
else
dist[i,j]:=inf;
can[j,i]:=can[i,j];
dist[j,i]:=dist[i,j];
end;
end;
{ поиск кратчайших путей между всеми парами вершин }
for k:=1 to n2 do
for i:=1 to n2 do
for j:=1 to n2 do
if dist[i,k]+dist[k,j]<dist[i,j] then
dist[i,j]:=dist[i,k]+dist[k,j];
По окончании работы этого алгоритма выполняется восстановление пути от источника до приемника. На каждом шаге нужно выбирать вершину, которая может быть достигнута из предыдущей (массив can) с минимальной длиной пути до приемника (массив dist).
