 Разбор задач отборочных командных соревнований школьников 2010
Разбор задач отборочных командных соревнований школьников 2010
 Разбор задачи G. Конфеты
Разбор задачи G. Конфеты
Тема: вывод формулыСложность: простая
Наихудшим вариантом по количеству конфет, при котором у Гомера не будет `K` конфет или более одного сорта, является вариант, когда у Гомера будет по `(K-1)` конфет каждого из `N` сортов. Но если к ним добавить хотя бы еще одну конфету, неважно какого сорта, то цель будет достигнута. Таким образом ответом на задачу будет значение `(K-1)*N+1`.
 Разбор задачи A. Потерянная страница
Разбор задачи A. Потерянная страница
Тема: вывод формулы или сортировкаСложность: простая
Ответ можно найти по формуле
`sum_{i=1}^n\ i\ -\ sum_{i=1}^{n-1}\ p_i`,
где `p_i` – номера собранных страниц. Эту формулу можно еще упростить, вспомнив следующую историю о детстве математика Гаусса.
Школьный учитель математики, чтобы занять первокласников на время, пока он будет занимать с другими учениками, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т.д., и мгновенно получил результат 5050.
Используя эту идею, можно легко найти сумму элементов любой арифметической прогрессии. Если выписать под последовательностью `a_1\ …\ a_n` те же элементы в обратном порядке, то суммы в каждом столбце будут одинаковы и равны `a_1\ +\ a_n`. В сумме этих `n` слагаемых каждый элемент исходной последовательности будет учтен дважды, поэтому результат сложения `(a_1\ +\ a_n)*n` нужно поделить на 2.
`sum_{i=1}^n\ a_i\ =\ {(a_1\ +\ a_n)*n}/2`
После применения формулы для суммы арифметической прогрессии получаем
`{(1\ +\ n)*n}/2\ \ -\ sum_{i=1}^{n-1}\ p_i`
Также для решения этой задачи можно применить сортировку расстановкой, работающую за время `O(n)`, или быструю сортировку, работающую за время `O(n\ log\ n)`. Использование сортировки пузырьком, работающей за время `O(n^2)`, приводит к превышению предела времени в тестах, где `n` велико.
 Разбор задачи C. Городской парад
Разбор задачи C. Городской парад
Тема: моделирование, очередьСложность: простая
Моделируем работу Виггама по регулированию движения платформ. На каждом шаге нужно выбрать одно из трех возможных действий:
- Отправить прибывшую платформу на площадь. Это можно сделать только в случае, когда номер прибывшей платформы равен номеру платформы, которую нужно отправить на площадь.
- Отправить первую платформу с боковой улицы на площадь. Это можно сделать только в случае, когда номер первой платформы на боковой улице равен номеру платформы, которую нужно отправить на площадь.
- Отправить прибывшую платформу на боковую улицу. Это можно сделать только в случае, если есть прибывшие платформы.
Если Виггам не может выполнить ни одно из этих действий, то печатаем сообщение "NO". Если все `N` платформ попали на площадь, печатаем сообщение "YES". Номера платформ на боковой улице нужно хранить в виде очереди.
var q,p:array[1..100] of integer;
i,pfirst,n,qfirst,qlast:integer;
begin
read(n);
for i:=1 to n do
read(p[i]);
qfirst:=1; { Индекс первого элемента в очереди }
qlast:=1; { Индекс первой свободной ячейки в очереди }
pfirst:=1; { Индекс элемента с номером прибывшей платформой }
i:=1; { Номер платформы, которую нужно отправлять на площадь }
while i<=n do
begin
if (pfirst<=n) and (p[pfirst]=i) then
begin { Отправить прибывшую платформу на площадь }
inc(pfirst);
inc(i);
end
else if (qfirst<qlast) and (q[qfirst]=i) then
begin { Отправить первую платформу с боковой улицы на площадь }
inc(qfirst);
inc(i);
end
else if (pfirst<=n) then
begin { Отправить прибывшую платформу на боковую улицу }
q[qlast]:=p[pfirst];
inc(qlast);
inc(pfirst);
end
else
begin { Нет больше платформ }
writeln('NO');
halt;
end;
end;
writeln('YES');
end.
 Разбор задачи F. Резервное копирование
Разбор задачи F. Резервное копирование
Тема: реализация заданного алгоритма, сортировка пузырькомСложность: ниже среднего
На первом этапе алгоритма необходимо отсортировать файлы в порядке уменьшения их размеров, сохраняя исходный порядок в случае одинакового размера. Такая сортировка называется стабильной. Сортировка пузырьком является стабильной, а быстрая сортировка или сортировка выбором – нет. В данном случае количество значений невелико (`N\ ≤\ 1000`), поэтому можно применить сортировку пузырьком, работающую за время `O(N^2)`.
type info=record i,s:longint; end;
var f:array[1..1000] of info; { вместо массива записей можно определить 2 массива }
tmp:info;
i,j,N,S,C:longint;
fl:boolean;
...
fl:=true;
while fl do
begin
fl:=false;
for i:=1 to N-1 do
if f[i].s<f[i+1].s then
begin
tmp:=f[i];
f[i]:=f[i+1];
f[i+1]:=tmp;
fl:=true;
end;
end;
Далее реализуем второй этап, как описано в задаче. Выравнивание размера файла на размер кластера можно реализовать, например, так:
cdsize[j]:=cdsize[j]-f[i].s; cdsize[j]:=cdsize[j]-cdsize[j] mod C;
 Разбор задачи D. Загрузка реактора
Разбор задачи D. Загрузка реактора
Тема: полный переборСложность: ниже среднего
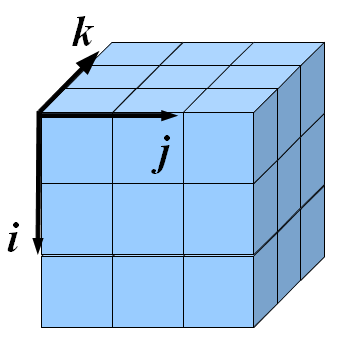
Для решения этой задачи нужно взять куб из блоков и отсечь от него все лишнее, как говорил Огюст Роден. Лишним в данном случае являются блоки в тех рядах, которые на соответствующих снимках обозначены символом '.'. Если какой-то блок не попадает ни на одном из снимков в пустой ряд, то этот блок нужно оставить, так как в задаче требуется определить максимально возможное количество блоков, находящихся в реакторе.
Нумерацию блоков в кубе будем делать в порядке, показанном на картинке. Стрелки указывают, в каком направлении будет возрастать соответствующий индекс в массиве.
var sn:array[1..3,1..20] of string; { снимки }
bl:array[1..20,1..20,1..20] of boolean; { куб из блоков }
i,j,k,kol,n:integer;
...
{ ввод данных }
readln(n);
for i:=1 to 3 do
for j:=1 to n do
readln(sn[i,j]);
{ заполнение куба }
for i:=1 to n do
for j:=1 to n do
for k:=1 to n do
bl[i,j,k]:=true;
{ отсечение лишнего }
for i:=1 to n do
for j:=1 to n do
for k:=1 to n do
if (sn[1,i][j]='.') or (sn[2,i][k]='.') or
(sn[3,n-k+1][j]='.') then
bl[i,j,k]:=false;
После отсечения лишнего могут появиться пустые ряды, находящиеся на снимках в местах, обозначенных символом '#'. Для обнаружения таких новых пустых рядов отметим на снимках символом '+' ряды, в которых есть хотя один блок. Если после таких изменений на снимках останется хоть один символ '#', значит в этом ряду после удаления лишних блоков не осталось ни одного, и, следовательно, на снимках есть противоречия.
kol:=0;
{ отметка символом '+' непустых рядов и подсчет числа блоков }
for i:=1 to n do
for j:=1 to n do
for k:=1 to n do
if bl[i,j,k] then
begin
sn[1,i][j]:='+';
sn[2,i][k]:='+';
sn[3,n-k+1][j]:='+';
inc(kol);
end;
{ поиск символов '#' на снимках }
for i:=1 to 3 do
for j:=1 to n do
for k:=1 to n do
if sn[i,j][k]='#' then
begin
writeln(-1);
halt(0);
end;
writeln(kol);
 Разбор задачи I. Ксилофон
Разбор задачи I. Ксилофон
Тема: вывод формулыСложность: средняя
Пусть `N=1`. Рассмотрим треугольники с длиной наибольшей стороны равной `i`. Длина второй по величине стороны `j` может принимать значения от `|__\ {i+3}/2\ __|` до `i-1`, т.е. `|__\ {i-2}/2\ __|` различных значений. Длина самой маленькой стороны может принимать значения от `i-j+1` до `j-1`, т.е. `2*j-i-1` различных значений. Количество возможных треугольников в зависимости от `j` является арифметической прогрессией. Чтобы найти сумму, можно воспользоваться формулой из задачи A. Сумма первого и последнего элемента прогрессии равна `2*|__\ {i-1}/2\ __|` (в правильности этого результата можно убедиться, взяв для `i` какое-то четное и нечетное значение, например, 9 и 10). Таким образом, количество возможных треугольников с длиной наибольшей стороны `i` равно `|__\ {i-2}/2\ __|*|__\ {i-1}/2\ __|`.
Если `N>1`, то часть треугольников исчезает, при этом либо число исчезающих треугольников (для `N\ ≤\ i/2`), либо число оставшихся треугольников (для `N\ >\ i/2`) также является арифметической прогрессией. Например, при `N\ ≤\ i/2` из подсчитанного ранее количества треугольников нужно вычесть `{(N-2)*(N-1)}/2`. Количество возможных треугольников при `N\ >\ i/2` определите самостоятельно.
Результат получаем суммированием количеств треугольников по всем `i` от `N+2` до `M`. Результат не превышает `M^3`, т.е. `(10^6)^3=10^18`, значит для вычислений необходимо использовать тип int64 (long long в C/С++).
 Разбор задачи K. Очистка озера
Разбор задачи K. Очистка озера
Тема: поиск в ширинуСложность: средняя
С помощью поиска в ширину находим минимальное число ходов от клетки с подъемником и от начальной клетки с роботом. Для поиска в ширину используется очередь.
var q:array[1..10000] of record i,j:integer; end;
dist:array[1..2,1..100,1..100] of integer;
map:array[1..100] of string;
q1,q2,n,m,r,c,d,e:longint;
{ выполнение хода в клетку (r,c), её достигли за di шагов из начальной позиции }
procedure move2(d,r,c,di:integer);
begin
if (r<1) or (r>n) or (c<1) or (c>m) then {нельзя} exit;
if map[r][c]='#' then {нельзя} exit;
if dist[d,r,c]>=0 then {уже были} exit;
dist[d,r,c]:=di;
{ добавляем в очередь }
q[q2].i:=r;
q[q2].j:=c;
inc(q2);
end;
procedure flood(r,c,d:integer);
var i,j,di:integer;
begin
for i:=1 to n do
for j:=1 to m do
dist[d,i,j]:=-1; { отмечаем, что не были }
q1:=1; { очередь пуста }
q2:=1;
move2(d,r,c,0); { помещаем в очередь стартовую позицию }
while q1<q2 do { очередь не пуста }
begin
{ берем первое значение из очереди }
i:=q[q1].i;
j:=q[q1].j;
inc(q1);
di:=dist[d,i,j]+1;
{ ходим во всех возможных направлениях }
move2(d,i+1,j,di);
move2(d,i-1,j,di);
move2(d,i,j+1,di);
move2(d,i,j-1,di);
end;
end;
...
flood(d,e,1);
flood(r,c,2);
Теперь нужно проверить два особых случая:
- робот не может дойти до подъемника (т.е. `"dist"[1,r,c]\ <\ 0`);
- все клетки, в которые может попасть робот, пусты, кроме клетки с подъемником.
В обоих случаях робот может не работать, выводим количество единиц мусора в клетке с подъемником и время 0.
В остальных случаях робот всегда должен носить мусор по одной единице в клетку с подъемником. Варианты с выбрасыванием мусора по пути, чтобы взять другой, не дают экономии времени, так как придется вернуться за выброшенным мусором. Поэтому все единицы мусора, кроме самой первой, робот собирает, отправляясь за ними из клетки с подъемником и затем возвращаясь в нее обратно по своим следам. Т.е. почти на каждую единицу мусора робот тратит `2*"dist"[1,i,j]` единиц времени, где `"dist"[1,i,j]` – количество ходов от клетки с подъемником до клетки `(i,j)`. Экономия времени может быть только за счет правильного выбора первой собираемой единицы мусора. При собирании первой единицы мусора робот проходит до нее `"dist"[2,i,j]` ходов вместо `"dist"[1,i,j]`, где `"dist"[2,i,j]` – количество ходов от начальной позиции робота до клетки `(i,j)`.
Таким образом минимальное время равно:
`sum_{AA\ i\ j\ :\ "dist"[1,i,j]≥0}\ 2*"map"[i][j]*"dist"[1,i,j]\ +\ min_{AA\ i\ j\ :\ "map"[i][j]≠'0'\ ^^\ "dist"[1,i,j]>0}\ ("dist"[2,i,j]-"dist"[1,i,j])`
 Разбор задачи H. Сдача
Разбор задачи H. Сдача
Тема: динамическое программирование, сложение и вывод длинных целыхСложность: средняя
Для сдачи суммы `i` монетами номиналом `b_1,\ …,\ b_j` есть следующие варианты:
- 0 монет номиналом `b_j`: способ сдать сумму `i` монетами номиналом `b_1,\ …,\ b_{j-1}`;
- 1 монета номиналом `b_j`: `b_j\ +` способ сдать сумму `i-b_j` монетами номиналом `b_1,\ …,\ b_{j-1}`;
- …
- `k=\ ⌊\ i//b_j\ ⌋` монет номиналом `b_j`: `k*b_j\ +` способ сдать сумму `i-k*b_j` монетами номиналом `b_1,\ …,\ b_{j-1}`.
Чтобы получить количество способов сдать сумму `i` монетами номиналом `b_1,\ …,\ b_j`, нужно просуммировать количество способов сдать сумму `i-k*b_j` монетами номиналом `b_1,\ …,\ b_{j-1}` для `k` от 0 до `⌊\ i//b_j\ ⌋`.
Количество способов будем хранить в таблице `T[i,\ j]`, где `i` – сумма сдачи, `j` – номер последнего использованного номинала.
`T[0,0]\ =\ 1`
`T[i,0]\ =\ 0`, если `i>0`
`T[i,\ j]\ =\ sum_{k=0}^{⌊\ i//b_j\ ⌋}\ T[i-k*b_j,\ j-1]`, если `j>0`
Вычисления можно существенно ускорить, используя следующее упрощение:
`T[i,\ j]\ =\ sum_{k=0}^{⌊\ i//b_j\ ⌋}\ T[i-k*b_j,\ j-1]\ =\ T[i,j-1]\ +\ sum_{k=1}^{⌊\ i//b_j\ ⌋}\ T[i-k*b_j,\ j-1]\ =\ T[i,j-1]\ +\ sum_{k=0}^{⌊\ i//b_j\ ⌋-1}\ T[i-b_j-k*b_j,\ j-1]\ =\ T[i,j-1]\ +\ T[i-b_j,\ j]`
Вместо матрицы для хранения результатов можно использовать вектор:
`T[i]=T[i]+T[i-b_j]`, для `i` от `b_j` до `S`.
Так как результат может быть очень большим, для вычислений нужно использовать длинную арифметику.
const mysize=25;
type mylong=array[1..mysize] of integer;
{ сложение длинных целых чисел }
procedure add(var a,b:mylong);
var i,p:integer;
begin
p:=0; { перенос }
for i:=1 to mysize do
begin
p:=p+a[i]+b[i];
b[i]:=p mod 10;
p:=p div 10;
end;
end;
{ вывод длинных целых чисел }
procedure print(var a:mylong);
var i:integer;
flg:boolean;
begin
flg:=false; { была ненулевая цифра? }
for i:=mysize downto 1 do
begin
if a[i]<>0 then
flg:=true;
if flg or (i=1) then
write(a[i]);
end;
end;
Основная часть программы выглядит так:
var T:array[0..10000] of mylong;
b:array[1..10] of integer;
i,j,n,s:integer;
...
read(s,n);
for i:=1 to n do
read(b[i]);
T[0][1]:=1;
for j:=1 to n do
for i:=b[j] to s do
add(T[i-b[j]],T[i]);
print(T[s]);
 Разбор задачи B. Вундеркинд
Разбор задачи B. Вундеркинд
Тема: модулярная арифметика, быстрое возведение в степень, периодические последовательностиСложность: выше среднего
Правила модулярной арифметики:
`(X+Y)\ mod\ M\ =\ ((X\ mod\ M)\ +\ (Y\ mod\ M))\ mod\ M`
`(X-Y)\ mod\ M\ =\ ((X\ mod\ M)\ -\ (Y\ mod\ M)\ +\ M)\ mod\ M` (в случае отрицательного результата нужно добавить к нему M)
`(X*Y)\ mod\ M\ =\ ((X\ mod\ M)\ *\ (Y\ mod\ M))\ mod\ M`
`X^P\ mod\ M\ =\ (X\ mod\ M)^P\ mod\ M`
Т.е. если к аргументам операций сложения, вычитания, умножения и возведения в степень применить остаток от деления, то результат не изменится. Это позволяет выполнять вычисления, не прибегая к длинной арифметике, в задачах, где требуется найти остаток от деления результата на `M`.
Для быстрого возведения в степень нужно воспользоваться способом, основанном на двоичном представлении показателя степени. Подобный способ, но для умножения чисел, был придуман еще 4 тысячи лет назад в Древнем Египте.
Известный российский математик Я.И.Перельман в своей книге «Занимательная арифметика» описал русский народный способ умножения. Сущность его в том, что умножение двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Например: нужно умножить 32 на 13. Это записывается таким образом:
`32*13`
`16*26`
`8*52`
`4*104`
`2*208`
`1*416`
Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Способ основан на том, что произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. А в результате многократного повторения этой операции получается искомое произведение: `32*13\ =\ 1*416`.
Если приходится делить нечетное число пополам, то в этом случае от нечетного числа откидывается единица и остаток уже делится пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Пример:
`19*17`
`9*34`
`1*272`
Сложив незачеркнутые числа, получаем правильный результат:
`17\ +\ 34\ +\ 272\ =\ 323`.
Обоснованность приема станет ясна, если принять во внимание, что
`19*17\ =\ (18\ +\ 1)*17\ =\ 18*17\ +\ 17`
`9*34\ =\ (8\ +\ 1)*34\ =\ 8*34\ +\ 34`, и так далее.
Ясно, что числа 17, 34 и т.п., утрачиваемые при делении нечетного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение.
У некоторых английских авторов этот способ умножения описывается под названием «русский крестьянский способ». В Германии крестьяне также пользуются им и называют его «русским».
Не исключено, что этот способ дошел до нас из Египта. Одним из основных источников сведений о древнеегипетской математике является папирус, купленный в Луксоре шотландским антикваром Александром Генри Риндом, который сейчас хранится в Британском музее. Папирус был найден в металлическом футляре. В развернутом виде имеет 5.5 м длины при 32 см ширины. Он представляет собой собрание решений 84 задач, имеющих прикладной характер. Папирус относится примерно к 2000-1700 г. до н.э. и представляет собой копию еще более древней рукописи, переписанную писцом Ахмесом. В папирусе используется иератическая система обозначений чисел – условные знаки, которые произошли из иероглифов в результате упрощений и стилизации. В нем есть четыре примера умножения, выполненные по способу, живо напоминающему наш народный русский способ. Вот один из них:

Что означает следующее:
9 1 /
18 2
36 4
72 8 /
= 81
Косая черта справа от строки указывает на то, что левое число будет добавлено к результату. Из этого примера видно, что египтяне пользовались приемом умножения, довольно сходным с нашим народным.
При возведении в степень нужно так же делить показатель степени, но вместо удвоения нужно выполнять возведение в квадрат и перемножать квадраты, связанные с нечетными числами. Все операции при этом выполняем по модулю `M`.
function powModM(A:int64; P:longint):longint;
var R:int64;
begin
R:=1;
while p>0 do
begin
if P mod 2=1 then
R:=(R*A) mod M;
A:=(A*A) mod M;
P:=P div 2;
end;
powModM:=R;
end;
Далее нужно найти `N`-е число в последовательности, и `N` может быть очень велико. Для устранения этой сложности воспользуемся принципом Дирихле или "принципом ящиков":
Если кролики рассажены в клетки, причём число кроликов больше числа клеток, то хотя бы в одной из клеток находится более одного кролика.
Все вычисления производятся по модулю `M`, поэтому `A_i` могут принимать только значения от 0 до `M-1`. Среди элементов последовательности с номерами от 0 до `M` существуют элементы `A_i` и `A_j`, такие что `i\ >\ j` и `A_i\ =\ A_j`, так как есть `M+1` элемент и `M` возможных значений. Следующее значение в последовательности зависит только от предыдущего, поэтому `∀\ k≥0` выполняется `A_{i+k}=A_{j+k}`. Т.е. после некоторого `j` последовательность будет повторяться с периодом равным `i-j`.
Чтобы найти `i` и `j`, можно отмечать в специальном массиве, на каком шаге было получено то или иное значение. Затем нужно убрать из `N` все периоды, повторяющиеся целое число раз, для этого нужно найти остаток от деления `N-j` на длину периода `i-j`.
var i,j,A0,B,P,N,M:longint;
step,A:array[0..100000] of longint;
...
for i:=0 to M-1 do
step[i]:=-1;
i:=0;
A[0]:=A0 mod M;
while (i<N) and (step[A[i]]<0) do
begin
step[A[i]]:=i;
A[i+1]:=(powModM(A[i],P)+B) mod M;
inc(i);
end;
if i<N then
begin
j:=step[A[i]];
i:=(N-j) mod (i-j) + j;
end;
writeln(A[i]);
Так как нас интересует только длина периода, то можно не искать начало периодической части, а найти такое `j`, для которого `A_j=A_M`. Длина периода будет равна `M-j`.
A[0]:=A0 mod M;
for i:=1 to M do
A[i]:=(powModM(A[i-1],P)+B) mod M;
if N<=M then
writeln(A[N])
else
begin
j:=M-1;
while A[j]<>A[M] do
dec(j);
writeln(A[(N-j) mod (M-j) + j]);
end;
 Разбор задачи E. Сигнальная система
Разбор задачи E. Сигнальная система
Тема: вычислительная геометрия, кратчайший путь между парами вершинСложность: выше среднего
Нужно отметить, что некоторые ограничения, получающиеся из реалистичности задачи, можно не учитывать в программе, так как требование минимизации количества отражений автоматически приводит к их выполнению.
Если луч дважды проходит через одно зеркало с отражением или без него, следовательно, путь луча можно сократить.
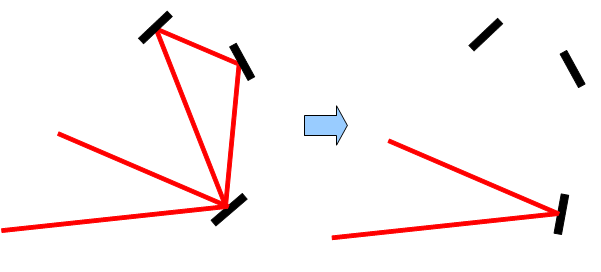 и
и 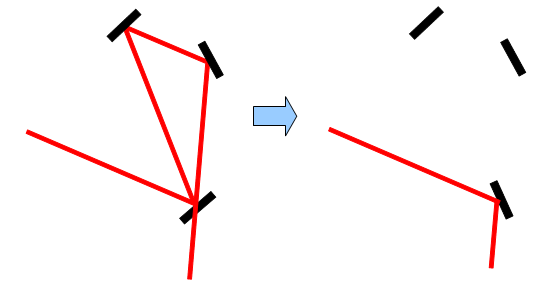
Если угол между падающим на зеркало лучом и отраженным равен 180 градусов, то такое зеркало можно просто убрать.

Для проверки пересечения луча с препятствиями можно воспользоваться либо общим алгоритмом, описанным в книге Кормена и др. "Алгоритмы: построение и анализ", либо написать самостоятельно алгоритм для пересечения с горизонтальным или вертикальным отрезком, который необходим в этой задаче. Рассмотрим только случай пересечения с вертикальным отрезком, так как для горизонтального отрезка нужно только поменять местами значения ординат и абсцисс при вызове функции. Перед рассмотрением вариантов необходимо обменять точки так, чтобы `x_1\ ≤\ x_2` и `y_3\ ≤\ y_4`.
Возможны следующие случаи:
- Отрезок `(x,y_3)-(x,y_4)` находится за пределами полосы, где находится отрезок `(x_1,y_1)-(x_2,y_2)`, т.е. `x\ <\ x_1` или `x\ >\ x_2`. Отрезки не пересекаются.
- Отрезок `(x_1,y_1)-(x_2,y_2)` также является вертикальным, т.е. `x_1\ =\ x_2\ =\ x`. Тогда отрезки пересекаются, если `y_4\ ≥\ y_1` и `y_3\ ≤\ y_2`.
- Отрезок `(x,y_3)-(x,y_4)` находится в полосе, где находится отрезок `(x_1,y_1)-(x_2,y_2)`. Используя подобие треугольников, найдем на отрезке `(x_1,y_1)-(x_2,y_2)` точку с абсциссой `x`: `y\ =\ y_1\ +\ {(y_2-y_1)*(x-x_1)}/{x_2-x_1}`. Отрезки пересекаются, если `y_3\ ≤\ y` и `y\ ≤\ y_4`. Чтобы избавиться от погрешностей вычислений, можно домножить все ординаты на `x_2-x_1` и проверять условие `y_3*(x_2-x_1)\ ≤\ y_1*(x_2-x_1)\ +\ (y_2-y_1)*(x-x_1)\ ≤\ y_4*(x_2-x_1)`.
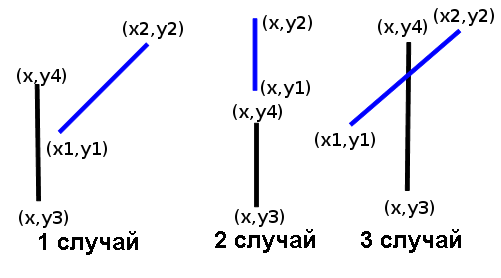
procedure swap(var a,b:longint);
var t:longint;
begin
t:=a;
a:=b;
b:=t;
end;
function iscross(x1,y1,x2,y2,x,y3,y4:longint):boolean;
var y:longint;
begin
if x1>x2 then
begin
swap(x1,x2);
swap(y1,y2);
end;
if y3>y4 then
swap(y3,y4);
if (x<x1) or (x>x2) then
begin { 1 случай }
iscross:=false;
exit;
end;
if x1=x2 then
begin { 2 случай }
if y1>y2 then
swap(y1,y2);
iscross:=(y4>=y1) and (y3<=y2);
exit;
end;
{ 3 случай }
y:=y1*(x2-x1)+(y2-y1)*(x-x1);
iscross:=(y3*(x2-x1)<=y) and (y<=y4*(x2-x1));
end;
Чтобы найти путь луча с минимальным количеством отражений (использованных зеркал), а среди них с минимальный длиной пути, можно искать кратчайший путь в графе, где длина ребра равна расстоянию между точками плюс `10^6`. Так число вершин в таком графе равно `N+2\ ≤\ 102` (`N` точек для установки зеркал, а также источник и приемник), то для поиска кратчайшего пути между источником и приемником можно использовать алгоритм Флойда-Уоршалла.
const inf:extended=1e100;
var dist:array[1..102,1..102] of extended;
can:array[1..102,1..102] of boolean;
...
{ составление матрицы с расстояниями }
for i:=1 to n2 do
begin
for j:=i to n2 do
begin
can[i,j]:=canlight(i,j);
if can[i,j] then
dist[i,j]:=1e6+sqrt(sqr(point[i].x-point[j].x)+sqr(point[i].y-point[j].y))
else
dist[i,j]:=inf;
can[j,i]:=can[i,j];
dist[j,i]:=dist[i,j];
end;
end;
{ поиск кратчайших путей между всеми парами вершин }
for k:=1 to n2 do
for i:=1 to n2 do
for j:=1 to n2 do
if dist[i,k]+dist[k,j]<dist[i,j] then
dist[i,j]:=dist[i,k]+dist[k,j];
По окончании работы этого алгоритма выполняется восстановление пути от источника до приемника. На каждом шаге нужно выбирать вершину, которая может быть достигнута из предыдущей (массив can) с минимальной длиной пути до приемника (массив dist).
 Разбор задачи J. Пластинки
Разбор задачи J. Пластинки
Тема: вычислительная геометрия, выявление особых точекСложность: высокая
Для решения задачи рассматриваем такие точки, которые могут находиться на видимой части какой-либо пластинки. Множество точек должно быть таким, чтобы на видимой части любой пластинки находилась хотя бы одна такая точка. При проверке каждой точки мы должны отметить в массиве флажков пластинку, оказавшуюся самой верхней в рассматриваемой точке. После проверок всех точек нужно подсчитать количество отмеченных пластинок – это и будет количество видимых пластинок.
Возможны следующие случаи расположения пластинок:
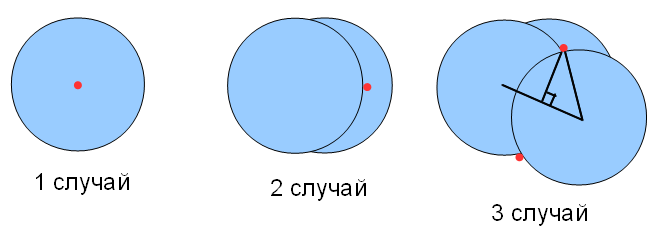
- Одиночная пластинка или несколько пластинок стопкой. Нужно проверить центр круга `(X_i,Y_i)`. Количество точек такого типа равно `N`.
- Одна пластинка накладывается на другую, при этом центр другой пластинки невидим. Нужно проверить точку, которая находится на расстоянии `R+ε` от центра первой пластинки по направлению к центру другой пластинки. Для нахождения координат точки нужно "масштабировать" вектор, соединяющий центры кругов – привести его к единичному, поделив обе координаты вектора на его длину, затем умножить координаты на новую длину. Координаты точки будут равны `(X_i+(X_j-X_i)*(R+ε)/D_{ij},\ Y_i+(Y_j-Y_i)*(R+ε)/D_{ij})`, где `j<i`, `D_{ij}` – расстояние между центрами пластинок `i` и `j`, `0\ <\ D_{ij}\ ≤\ R`, `ε=10^{-6}`. Количество точек такого типа не превышает `N*(N-1)/2`.
- Пластинку накрывает две или больше пластинок. Видимая часть накрытой пластинки представляет собой "многоугольник", образованный дугами краев накрывающих пластинок и, возможно, края самой пластинки. Нужно проверить 2 точки, лежащие на расстоянии `ε` от двух точек пересечения краев накрывающих пластинок. Для нахождения координат точек выполняем поворот на `90°` и `-90°` и масштабирование вектора, соединяющий центры кругов. Расстояние `P` от точек пересечения до середины отрезка, соединяющего центры кругов, равно `sqrt(R^2\ -\ D_{ij}^2/4)`. Середина отрезка между центрами кругов имеет координаты `((X_j+X_i)/2,\ (Y_j+Y_i)/2)`. Координаты точек равны `((X_j+X_i)/2\ -\ (Y_j-Y_i)*(P+ε)/D_{ij},\ (Y_j+Y_i)/2\ +\ (X_j-X_i)*(P+ε)/D_{ij})` и `((X_j+X_i)/2\ +\ (Y_j-Y_i)*(P+ε)/D_{ij},\ (Y_j+Y_i)/2\ -\ (X_j-X_i)*(P+ε)/D_{ij})`, где `j<i`, `0\ <\ D_{ij}\ ≤\ 2*R`, `ε=10^{-6}`. Количество точек такого типа не превышает `N*(N-1)`.
Проверка каждой точки выполняется за время `O(N)`. Всего точек `O(N^2)`, значит алгоритм будет работать за время `O(N^3)`.

 Начало
Начало Соревнования
Соревнования