Начало
Соревнования
6. Треугольник Максима
Задача средней сложности.
Пусть `P` – частота предыдущей ноты, а `T` – текущей.
Если `P<T`, а результат сравнения равен closer, то возможная частота звучания треугольника будет лежать в интервале `[(P+T)/2,\ +∞)`, отмеченному цветом на рисунке.
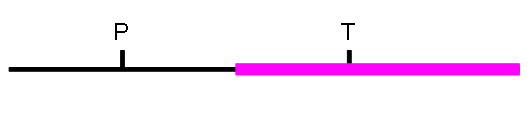
Априори частота треугольника лежит в диапазоне `d=[30,\ 4000]`. После получения результата очередного сравнения этот диапазон меняется:
| Расположение частот | Результат сравнения | Изменение диапазона |
| `P<T` | closer | `d=d∩[(P+T)/2,\ +∞)` |
| `P>T` | further | `d=d∩[(P+T)/2,\ +∞)` |
| `P<T` | further | `d=d∩(-∞,\ (P+T)/2]` |
| `P>T` | closer | `d=d∩(-∞,\ (P+T)/2]` |
Если `P=T`, никаких действий не выполняется.
uses math;
var a,b,p,t:extended;
n,i:integer;
s:string;
begin
read(n);
readln(p);
a:=30;
b:=4000;
for i:=2 to n do
begin
readln(t,s);
if p=t then
else if (p<t) and (s=' closer') or (p>t) and (s=' further') then
a:=max(a,(p+t)/2.0)
else
b:=min(b,(p+t)/2.0);
p:=t;
end;
writeln(a:1:6,' ',b:1:6);
end.
