 Разбор задач
Разбор задач
 1. Соревнование картингистов
1. Соревнование картингистов
Простая задача на технику программирования.
Так как ввод содержит смесь тестовых и числовых данных, при вводе нужно правильно использовать операторы read/readln, чтобы не произошло ошибки ввода-вывода.
var
winname,name:string;
t,sumt,wintime:longint;
n,m,i,j:integer;
begin
readln(n, m);
wintime := 100001;
winner := '';
for i := 1 to n do
begin
readln(name);
sumt := 0;
for j := 1 to m do
begin
read(t);
sumt := sumt + t;
end;
readln;
if (sumt < wintime) then
begin
wintime := sumt;
winname := name;
end;
end;
writeln(winname);
end.
 2. Дипломы
2. Дипломы
Задача средней сложности.
Количество дипломов, которые можно разместить вдоль одной из сторон квадратной доски, не превосходит `sqrt(n)`. Если вдоль вертикальной стороны квадратной доски размещено `a` дипломов, а вдоль горизонтальной – `b` дипломов, тогда общее число дипломов составляет `a*b\ ≤\ n`. Если оба числа a и b больше `sqrt(n)`, тогда `a*b\ >\ n`. Получили противоречие, следовательно, либо `a\ ≤\ sqrt(n)`, либо `b\ ≤\ sqrt(n)`.
Мы должны для всех `k` от 1 до `sqrt(n)` определить размер доски при размещении `k` дипломов вдоль вертикальной или вдоль горизонтальной стороны квадрата.
uses math;
var n,w,h,s,m:int64;
k,sn:integer;
begin
read(w,h,n);
sn:=trunc(sqrt(n))+1;
s:=(w+h)*n;
for k:=1 to sn do
begin
m:=(n+k-1) div k; { целочисленное деление с округлением вверх }
s:=min(s,max(k*w,m*h)); { k дипломов по горизонтали }
s:=min(s,max(m*w,k*h)); { k дипломов по вертикали }
end;
writeln(s);
end.
Другой вариант – с помощью двоичного поиска найти наименьшую длину стороны квадрата, которая позволит разместить `n` дипломов.
uses math;
var n,w,h,a,b,c:int64;
k:extended;
begin
read(w,h,n);
a:=0; { в квадрате со стороной a не должно гарантированно поместиться n дипломов }
b:=n*max(w,h); { в квадрате со стороной b должно гарантированно поместиться n дипломов }
while a<b do
begin
c:=(b+a) div 2; { пробная длина стороны квадрата посредине между a и b }
k:=c div w; { предотвращение переполнения }
k:=k*(c div h); { при вычислениях }
{ k - количество дипломов, которое поместится в квадрате со стороной c }
if k>=n then b:=c { изменяем верхнюю границу }
else a:=c+1; { изменяем нижнюю границу }
end;
{ a=b }
writeln(a);
end.
 3. Булева функция
3. Булева функция
Задача средней сложности.
Самый универсальный способ решения – использовать динамическое программирование.
Для этого заполняем таблицу `T_{ij}` максимальным количеством единиц среди `i` булевских значений, таких что результат цепного вычисления равен `j`. Для получения результата нужно выполнить обратную трассировку по таблице.
var
n,i,j,k,b:longint;
t,h1,h2:array[1..100000,0..1] of longint;
f:string;
s:array[1..100000] of integer;
begin
readln(n);
readln(f);
{ заполнение таблицы }
t[1,0]:=0;
t[1,1]:=1;
h2[1,0]:=0;
h2[1,1]:=1;
for i:=2 to n do
begin
t[i,0]:=-1;
t[i,1]:=-1;
for j:=0 to 1 do
for k:=0 to 1 do
begin
b:=ord(f[j*2+k+1])-ord('0'); { вычисляем значение f(j,k) }
if (t[i-1,j]>=0) and (t[i,b]<t[i-1,j]+k) then
begin
t[i,b]:=t[i-1,j]+k;
h1[i,b]:=j; { запоминаем способ }
h2[i,b]:=k; { получения результата }
end;
end;
end;
{ обратная трассировка }
if t[n,1]<0 then
writeln('No solution')
else
begin
j:=1;
for i:=n downto 1 do
begin
s[i]:=h2[i,j];
j:=h1[i,j];
end;
for i:=1 to n do
write(s[i]);
writeln;
end;
end.
Другой способ решения – рассмотреть все возможные варианты для функции `f`. Всего может быть 16 вариантов задания этой функции, но все они сводятся к следующим пяти случаям.
| Булева функция | Последовательность |
| ???1 | 111...111 |
| 1??0 | 111...110 |
| 01?0 | 111...101 для четных `n` и 111...111 для нечетных `n` |
| 0010 | 100...000 |
| 0000 | No solution |
 4. Кольцевая автодорога
4. Кольцевая автодорога
Сложная задача на геометрию.
Возможны следующие случаи взаимного расположения достопримечательностей и автодороги:
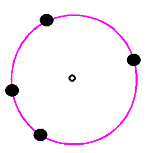 | Достопримечательности расположены на одной окружности. Количество вариантов постройки кольцевой автодороги – бесконечно, радиус наименьшей равен 0. |
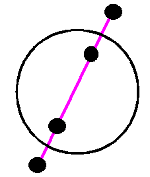 | Достопримечательности лежат на одной прямой и внутренние точки равноудалены от внешних. Количество вариантов постройки кольцевой автодороги – бесконечно. |
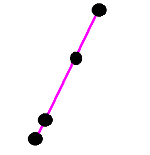 | Достопримечательности лежат на одной прямой, но внутренние точки не равноудалены от внешних. Количество вариантов постройки кольцевой автодороги – ноль. |
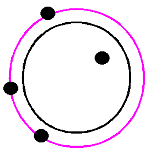 | Три достопримечательности расположены на одной окружности, а одна – снаружи или внутри нее. Нужно рассмотреть 4 таких варианта. |
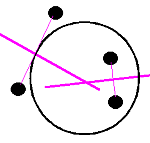 | Точки серединного перпендикуляра к отрезку, соединяющему две точки, равноудалены от этих точек. Точка пересечения двух перпендикуляров является центром автодороги. Нужно рассмотреть 3 таких варианта. |
 5. Миша и негатив
5. Миша и негатив
Простая задача на технику программирования.
Пиксели в негативе будут ошибочны, если они будут совпадать с исходным пикселями в исходном изображении.
var a,b:array[1..100] of string;
n,m,i,j,k:integer;
begin
readln(n,m);
for i:=1 to n do
readln(a[i]);
readln; { пропуск пустой строки }
for i:=1 to n do
readln(b[i]);
k:=0;
for i:=1 to n do
for j:=1 to m do
if a[i][j]=b[i][j] then inc(k);
writeln(k);
end.
 6. Треугольник Максима
6. Треугольник Максима
Задача средней сложности.
Пусть `P` – частота предыдущей ноты, а `T` – текущей.
Если `P<T`, а результат сравнения равен closer, то возможная частота звучания треугольника будет лежать в интервале `[(P+T)/2,\ +∞)`, отмеченному цветом на рисунке.
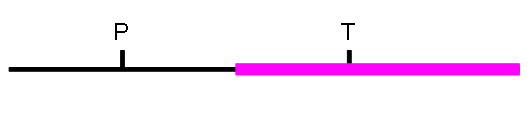
Априори частота треугольника лежит в диапазоне `d=[30,\ 4000]`. После получения результата очередного сравнения этот диапазон меняется:
| Расположение частот | Результат сравнения | Изменение диапазона |
| `P<T` | closer | `d=d∩[(P+T)/2,\ +∞)` |
| `P>T` | further | `d=d∩[(P+T)/2,\ +∞)` |
| `P<T` | further | `d=d∩(-∞,\ (P+T)/2]` |
| `P>T` | closer | `d=d∩(-∞,\ (P+T)/2]` |
Если `P=T`, никаких действий не выполняется.
uses math;
var a,b,p,t:extended;
n,i:integer;
s:string;
begin
read(n);
readln(p);
a:=30;
b:=4000;
for i:=2 to n do
begin
readln(t,s);
if p=t then
else if (p<t) and (s=' closer') or (p>t) and (s=' further') then
a:=max(a,(p+t)/2.0)
else
b:=min(b,(p+t)/2.0);
p:=t;
end;
writeln(a:1:6,' ',b:1:6);
end.
 7. Производство деталей
7. Производство деталей
Задача средней сложности на графы.
Для решения этой задачи можно использовать топологическую сортировку, т.е. размещение графа вдоль прямой таким образом, что все дуги были направлены слева направо. При этом достаточно упорядочить только вершины, достижимые из вершины 1.
Для хранения графа будем использовать два массива: массив d с номерами необходимых для производства деталей, записанных последовательно друг за другом, сначала для 1-й, затем для 2-й, и т.д., и массив f, в котором для i-й детали хранится номер начала последовательности номеров необходимых деталей в первом массиве, т.о. номера деталей, необходимых производства для i-й детали, хранятся в ячейках d[f[i]], d[f[i]+1], …, d[f[i+1]-1].
var
p:array[1..100000] of longint; { время на производство }
s:array[1..100000] of longint; { топологически упорядоченная последовательность }
d:array[1..200000] of longint; { необходимые детали для производства }
f:array[1..100001] of longint; { номера начал в массиве d }
u:array[1..100000] of boolean; { деталь уже произвели? }
n,i,j,k,m:longint;
t:int64; { общее время производства }
{ алгоритм топологической сортировки }
procedure topsort(i:longint);
var j:longint;
begin
if u[i] then exit;
for j:=f[i] to f[i+1]-1 do
topsort(d[j]);
u[i]:=true;
inc(m);
s[m]:=i;
end;
begin
{ ввод данных }
read(n);
for i:=1 to n do
read(p[i]);
m:=1;
for i:=1 to n do
begin
read(k);
f[i]:=m;
for j:=1 to k do
begin
read(d[m]);
inc(m);
end;
end;
f[n+1]:=m;
{ топологическая сортировка }
m:=0;
topsort(1);
{ расчет суммарного времени }
t:=0;
for i:=1 to m do
t:=t+p[s[i]];
{ вывод ответа }
writeln(t,' ',m);
for i:=1 to m do
write(' ',s[i]);
writeln;
end.
 8. Новое слово в рекламе
8. Новое слово в рекламе
Сложная задача на работу со строками.
Будем перебирать все возможные `K` от 1 до `|s|`, пока набор из `K` блоков, содержащих заданное слово `s`, не будет найден.
Назовем `K`-подсловом `w_j`, где `j` от 1 до `K`, последовательность букв из `s` вида `s_j\ s_{K+j}\ s_{2K+j}\ …`.
Для каждого `K` заполняем массив `T`[1..`L`, 1..`K`] следующим образом. Вначале массив инициализируется нулями. Затем устанавливаем `T`[`i,j`]=`m`, если `K`-подслово `w_j` начинается с позиции `i` в блоке `B_m`. Заполнения массива `T` выполняется за время `O(K*N*L*|s|/K)=O(|s|*N*L)`.
var s:string;
b:array[1..100] of string; { блоки }
T:array[1..100,1..200] of integer;
n,L,i,j,k,m,p,q,wlen,slen:integer;
flg:boolean;
...
slen:=length(s);
for k:=1 to length(s) do
begin
{ заполнение таблицы T }
for i:=1 to L do
for j:=1 to k do
T[i,j]:=0;
for j:=1 to k do
begin
wlen:=(slen-j+k) div k; { длина j-го K-подслова }
for i:=1 to L-wlen+1 do
for m:=1 to n do
begin
{ проверяем, что j-е K-подслово начинается с позиции i в блоке m }
p:=j;
q:=i;
while (p<=slen) and (b[m][q]=s[p]) do
begin
inc(q);
p:=p+k;
end;
if p>slen then
begin
T[i,j]:=m;
break;
end;
end;
end;
...
end;
writeln(-1);
После этого мы должны найти в этом массиве последовательность из `K` ненулевых ячеек, начиная с некоторой ячейки `(i,j)`: `T`[`i,j`] `T`[`i,j+1`] … `T`[`i,K`] `T`[`i-1,1`] … `T`[`i-1,j-1`]. Номера блоков в этих ячейках образуют требуемый набор блоков. Поиск последовательности из `K` ненулевых ячеек в массиве `T` можно выполнить за время `O(L*K)`, если при обнаружении нулевой ячейки сдвигаться на `K` позиций от нее.
i:=1;
j:=1;
while i<=L do
begin
flg:=true;
for p:=j to k do
if T[i,p]=0 then
begin
flg:=false;
i:=i+1;
j:=p;
break;
end;
if flg then
for p:=1 to j-1 do
if T[i-1,p]=0 then
begin
flg:=false;
j:=p;
break;
end;
if flg then
begin
{ вывод ответа }
writeln(k);
for p:=j to k do
write(' ',T[i,p]);
for p:=1 to j-1 do
write(' ',T[i-1,p]);
writeln;
halt(0);
end;
end;
Общее время работы алгоритма равно `O(|s|*(|s|*N*L+K*L))=O(|s|^2*N*L)`.

 Начало
Начало Соревнования
Соревнования