 Задачи командных соревнований для школьников 1998
Задачи командных соревнований для школьников 1998
1. Power Crisis
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
During the power crisis in New Zealand this winter (caused by a shortage of rain and
hence low levels in the hydro dams), a contingency scheme was developed to turn
off the power to areas of the country in a systematic, totally fair, manner.
The country was divided up into `N` regions (Auckland was region number 1, and Wellington number 13).
A number, `m`, would be picked "at random", and the power would first be turned off in
region 1 (clearly the fairest starting point) and then in every `m`'th region after that,
wrapping around to 1 after `N`, and ignoring regions already turned off. For
example, if `N=17` and `m=5`, power would be turned off to the regions in the
order: 1, 6, 11, 16, 5, 12, 2, 9, 17, 10, 4, 15, 14, 3, 8, 13, 7.
The problem is that it is clearly fairest to turn off Wellington last (after all,
that is where the Electricity headquarters are), so for a given `N`, the "random" number `m` needs to
be carefully chosen so that region 13 is the last region selected.
Write a program that will read in the number of regions and then determine the
smallest number `m` that will ensure that Wellington (region 13) can function while the rest of the country is blacked out.
Input will consist of the number of regions (`N`) with `13\ ≤\ N\ <\ 100`.
Output will consist of the number `m` according to the above scheme.
Source: New Zealand Contest, 1992
2. Разноцветный треугольник
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
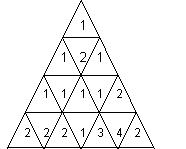
Из разноцветных плиток (количество цветов не более 9),
имеющих форму равностороннего треугольника, произвольным образом выложен большой
равносторонний треугольник со стороной в `k` раз большей размера плитки.
Требуется определить, сколько в большом треугольнике образовалось различных треугольников,
состоящих из плиток одного цвета, со стороной вдвое большей размера плитки.
Примечание
На рисунке показан выложенный из плиток треугольник со стороной в 4 раза большей размера плитки.
Цвет каждой плитки условно обозначен цифрами от 1 до 9. Для данного примера количество всевозможных
треугольников со стороной 2, состоящих из плиток одного цвета равно 2.
Формат ввода
В первой строке длина стороны `k` (`1\ <\ k\ ≤\ 10`) большого треугольника,
в последующих `k` строках через пробел указатели цвета плитки горизонтального ряда в порядке слева направо.
Ряды плиток большого треугольника описываются последовательно, начиная с его вершины.
Формат вывода
Вывести одно число – количество одноцветных треугольников со стороной 2.
Пример ввода
4
1
1 2 1
1 1 1 1 2
2 2 2 1 3 4 2
3. Наименьшее общее кратное
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (1)
Найти наименьшее общее кратное набора из `N` целых чисел, лежащих в диапазоне от 1 до 1000.
Под наименьшим общим кратным набора чисел понимается наименьшее из таких чисел, которые делятся на любое из чисел набора.
Формат ввода
В первой строке задается количество чисел `N` (`1\ ≤\ N\ ≤\ 20`) в наборе.
Во второй строке перечисляются через пробел в любом порядке все `N` целых чисел набора.
Формат вывода
Вывести полученное наименьшее общее кратное для заданного набора чисел.
4. Двоичная дробь
Ограничения: время – 1s/2s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Пусть правильная дробь задана двумя двоичными числами `a` и `b`, числителем и знаменателем соответственно,
где `1\ ≤\ a\ <\ b\ ≤\ 9999`. Необходимо написать программу, которая вычисляла бы непериодическую часть и
период двоичной дроби. Если дробь конечная, считать, что ее период состоит из нуля.
Примечание
Любая правильная дробь `a/b` в двоичной системе счисления записывается в общем случае в виде бесконечной
дроби 0,<непериодическая часть>(<период>) .
Например, `(5/12)_10\ =\ (0,01(10)\ )_2`. Здесь 01 – непериодическая часть, (10) – период дроби.
Формат ввода
В первой строке находится двоичное число `a`; во второй строке – двоичное число `b`.
Формат вывода
Вывести двоичную дробь в формате, как показано в примере вывода.
5. Шиворот-навыворот
Ограничения: время – 200ms/500ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (1)
Написать программу, печатающую все слова введенного текста наоборот.
Словом считается последовательность прописных и строчных русских букв (ASCII-коды от 128 до 255) и дефиса,
обозначаемого символом '-' (минус).
Остальные символы остаются в предложении без изменений на своих местах.
Формат ввода
В первой строке содержится исходный текст (не более 80 символов).
Формат вывода
В первую строку выводится текст с реверсированными словами.
Пример ввода
Лучший подарок, по-моему, мёд. Каждый осёл это сразу поймёт!
Пример вывода
йишчуЛ корадоп, умеом-оп, дём. йыджаК лёсо отэ узарс тёмйоп!
6. Puzzle для компьютера
Ограничения: время – 2s/4s, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Прямоугольная картинка разрезана на несколько одинаковых прямоугольных кусочков.
Необходимо собрать исходную картинку, стыкуя кусочки таким образом,
чтобы рисунок на соприкасающихся кусочках совпадал. Кусочек головоломки для компьютера
будем представлять в виде массива 4x8 символов.
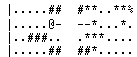 |
Символы на краях этих кусочков совпадают, поэтому их можно состыковать. |
Исходная картинка для упрощения окружена рамкой из символов
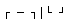
(с ASCII-кодами
218, 196, 191, 179, 192 и 217 соответственно),
которые не встречаются нигде больше в рисунке. Картинку можно собрать единственным способом.
Формат ввода
В первой строке размеры головоломки в кусочках: число рядов `N` и (через пробел) число столбцов `M` (`2\ ≤\ N,\ M\ ≤\ 5`).
В последующих `4*N` строках содержится по `8*M` символов – это кусочки (размером 4x8 символов),
из которых необходимо собрать головоломку.
Формат вывода
В выходной файл вывести собранную картинку.
| Пример ввода (сетка нарисована для удобства) |
3 4
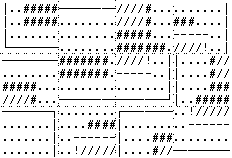 |
| Пример вывода |
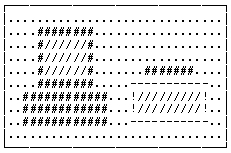 |
 Задачи командных соревнований для школьников 1998
Задачи командных соревнований для школьников 1998 Реализация заданного алгоритма
Реализация заданного алгоритма

 Полный перебор
Полный перебор


 Сложение и вычитание длинных целых, умножение и деление на короткое
Сложение и вычитание длинных целых, умножение и деление на короткое

 Системы счисления с другим основанием
Системы счисления с другим основанием

 Автоматы
Автоматы

 Рекурсивный перебор
Рекурсивный перебор

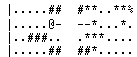
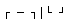 (с ASCII-кодами
218, 196, 191, 179, 192 и 217 соответственно),
которые не встречаются нигде больше в рисунке. Картинку можно собрать единственным способом.
(с ASCII-кодами
218, 196, 191, 179, 192 и 217 соответственно),
которые не встречаются нигде больше в рисунке. Картинку можно собрать единственным способом.


 Начало
Начало Соревнования
Соревнования