Начало
Соревнования
Задачи региональной олимпиады по информатике 1998
1. Кубики
Вывод формулыОлимпиадные задачи на русском языке
| 26/04/1998 | Региональная олимпиада Информатика-1998 (1) |
| 10/09/2011 | Занятие 1 (A) |
Ограничения: время – 200ms/500ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Маленький Метью очень любил играть в кубики.
Он делал столбики из кубиков и ставил эти столбики
на квадратный столик (не случайным образом, а в клетки, если представить
столик разлинованным на клетки по размерам кубиков).
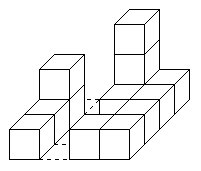
Из-за маленького роста Метью мог построить столбики не
более 8 кубиков. На рисунке можно увидеть одно из его творений
на столике размером 4x4.
Понравившиеся ему строения он зарисовывал. Но так как он не умел рисовать
3D-изображения, то ограничивался видом спереди и видом справа.
Метью думал, что этой информации достаточно, чтобы построить
это строение снова (но он никогда не пытался сделать это).
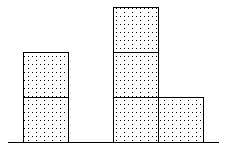
 Вид спереди | 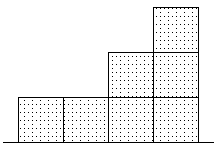 Вид справа |
Через несколько лет, рассматривая рисунки, он понял,
что можно построить более чем одно строение с тем же самым видом
спереди и справа.
Метью обнаружил, что существует
некоторое "минимальное" из всех возможных строение
с минимальным числом кубиков `N` и "максимальное" с числом кубиков `M`.
Для показанного примера "минимальное" строение содержит `N=7` кубиков,
а "максимальное" – `M=17` кубиков.
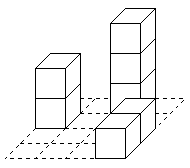
 Минимальное строение | 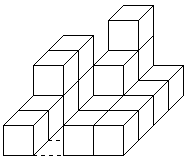 Максимальное строение |
Напишите программу, которая позволяет вычислить
максимальное (`M`) и минимальное (`N`) число кубиков для строения,
задаваемого видами спереди и справа.
Входной файл содержит в первой строке размеры столика `K` (`1\ ≤\ K\ ≤\ 8`),
во второй строке – `K` чисел через пробел: высота столбиков (от 0 до 8)
на виде спереди, в третьей строке также `K` чисел – высота столбиков
на виде справа. Известно, что по этим исходным данным
можно построить как минимум одно строение.
В выходной файл вывести числа `N` и `M` через пробел.
Пример ввода
4 2 0 3 1 1 1 2 3
Пример вывода
7 17
2. Рыба!
Эйлеров путь/циклОлимпиадные задачи на русском языке
| 26/04/1998 | Региональная олимпиада Информатика-1998 (2) |
| 13/03/2010 | Занятие 10 (A) |
| 17/12/2013 | Занятие 12 для начинающих (D) |
| 17/07/2019 | Лето 2019 - 8 (D) |
Ограничения: время – 500ms/1000ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
Дан набор косточек домино. Требуется определить,
можно ли составить из всех косточек набора
непрерывную цепочку по обычным правилам игры в домино
(т.е. стыкуя стороны с одинаковым числом очков).
Входной файл содержит в первой строке число косточек в наборе `N` (`1\ ≤\ N\ ≤\ 100`),
далее `N` строк с парами чисел `i` `j` (`0\ ≤\ i,\ j\ ≤\ 6`), соответствующих
косточке домино.
В выходном файле должен быть ответ YES или NO.
Пример ввода 1
3 1 2 3 4 2 3
Пример вывода 1
YES
Пример ввода 2
2 1 2 3 4
Пример вывода 2
NO
3. Ход конем
Поиск в ширину (BFS)Олимпиадные задачи на русском языке
| 26/04/1998 | Региональная олимпиада Информатика-1998 (3) |
| 27/02/2010 | Занятие 8 (D) |
| 09/12/2010 | Сборы: Общий итог (4D) |
| 30/12/2010 | Сборы 4: Домашнее задание (D) |
| 30/12/2010 | Сборы 4: Практика (D) |
| 03/07/2019 | Лето 2019 - 2 (A) |
Ограничения: время – 500ms/1000ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
На доске 8x8 некоторые клетки произвольным образом
покрашены в черный цвет (кроме верхнего левого и правого нижнего угла доски).
Требуется определить имеется ли путь для шахматного коня
из верхнего левого в правый нижний угол доски, не проходящий по черным клеткам, и минимальное количество ходов, требующееся для этого.
Входной файл содержит 8 строк по 8 символов.
Белая клетка кодируется символом '.' (точка), а черная – символом '#'.
В выходной файл записывается ответ NO или YES. При положительном ответе кроме того выводится через пробел число ходов.
Пример ввода 1
......## .....##. ....##.. ...##... ..##.... .##..... ##...... #.......
Пример вывода 1
YES 6
Пример ввода 2
.#.#.#.# #.#.#.#. .#.#.#.# #.#.#.#. .#.#.#.# #.#.#.#. .#.#.#.# #.#.#.#.
Пример вывода 2
NO
4. Карданный вал
Вычислительная геометрияОлимпиадные задачи на русском языке
| 26/04/1998 | Региональная олимпиада Информатика-1998 (4) |
| 10/09/2011 | Занятие 1 (B) |
Ограничения: время – 200ms/500ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод
Послать решение Blockly Посылки Темы Где Обсудить (0)
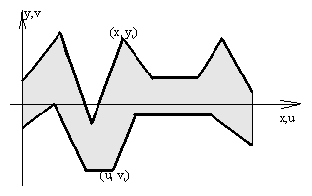
Напишите программу для определения объема отливки.
Отливка имеет форма прямой призмы с высотой `h`, а форма основания
определяется двумя непересекающимися ломаными линиями.
Входной файл содержит в первой строке высоту `h` (`0\ <\ h\ ≤\ 10`),
во второй строке – количество отрезков в верхней ломаной `n` (`1\ ≤\ n\ ≤\ 50`),
далее следует `n+1` строка с координатами точек верхней ломаной `x_i\ y_i`
через пробел. Точки перечислены в порядке возрастания координаты `x_i`,
таким образом линия `(x_{i-1}\ y_{i-1})-(x_i\ y_i)` является `i`-м
отрезком ломаной (`i=1…n`). Далее идет количество отрезков
в нижней ломаной `m` (`1\ ≤\ m\ ≤\ 50`), затем `m+1` строка с координатами
точек ломаной `u_i\ v_i` через пробел.
Все координаты и высота `h` целые, не превосходящие по модулю 100,
кроме того `x_0=u_0=0` и `x_n=u_m`, `x_{i-1}\ ≤\ x_i`, `u_{i-1}\ ≤\ u_i`.
В выходной файл вывести результат с точностью `10^{-2}`.
Пример ввода
4 2 0 1 5 6 10 1 3 0 -5 2 0 8 0 10 -5
Пример вывода
180.00
