 Задачи 2 лиги областной олимпиады школьников по информатике 2002
Задачи 2 лиги областной олимпиады школьников по информатике 2002
 1. Числа Фибоначчи
1. Числа Фибоначчи
Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Последовательность чисел Фибоначчи определяется следующим образом: `F_0=0`, `F_1=1`,
`F_n\ =\ F_{n-1}\ +\ F_{n-2}` для `n>1`. Последовательность можно
определить и для отрицательных индексов `n`. Вот ближайшие к нулю
числа Фибоначчи:
| `n` | … | –6 | –5 | –4 | –3 | –2 | –1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| `F_n` | … | –8 | 5 | –3 | 2 | –1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
Во входном файле содержится три строки. В первой строке содержится
целое число `d` (`0\ ≤\ d\ ≤\ 9`). Во второй строке содержится целое
число `a`, а в третьей строке – целое число `b` (`-10^6\ ≤\ a\ ≤\ b\ ≤\ 10^6`).
В выходной файл вывести единственное целое число – количество чисел, оканчивающихся на
заданную цифру `d`, среди чисел Фибоначчи с индексами
в диапазоне от `a` до `b` включительно.
 2. Холмы и равнины
2. Холмы и равнины
Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Среди результатов измерений высот найти самую длинную непрерывную
подпоследовательность, состоящую из одинаковых чисел. Если существуют
несколько таких подпоследовательностей с одинаковой длиной,
выбрать подпоследовательность, состоящую из бОльших чисел, т.е. большей высоты.
Из двух подпоследовательностей одинаковой длины и одинаковой высоты
выбрать подпоследовательность, которая начинается в
последовательности измерений раньше.
Во входном файле в первой строке содержится целое число `n` (`1\ ≤\ n\ ≤\ 100\ 000`) – число
измерений, далее следует `n` строк, содержащих по одному целому числу (от –10000 до 10000) в
строке.
В выходной файл вывести номер первого элемента первой
самой высокой из самых длинных
непрерывных подпоследовательностей из одинаковых чисел.
Пример ввода
6
3000
2002
2002
2002
-4500
-4500
 3. Дроби
3. Дроби
Ограничения: время – 1s/2s, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Периодическая десятичная дробь обычно записывается в виде:
целая_часть , непериодическая_часть ( период ). Любая простая дробь может быть представлена в виде десятичной периодической дроби и наоборот. Например, десятичная дробь 0,2(45) соответствует дроби
`27/110`, так как
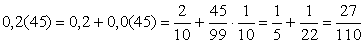
.
Во входном файле в первой строке содержится периодическая десятичная дробь `x` (`\ 0\ <\ x\ <\ 1`), общее количество цифр в периоде и непериодической части дроби не превосходит 9.
В выходной файл вывести представление дроби `x` в виде простой дроби `p`/`q`, где `p` и `q` являются взаимно простыми целыми числами.
 4. Число соответствий
4. Число соответствий
Ограничения: время – 200ms/500ms, память – 64MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
Числом соответствий для двух строк `a` и `b` будем называть максимально
возможное количество пар `(a_i,\ b_j)`, образованных из `i`-го символа строки `a` и `j`-го символа строки `b`, таких, что `a_i=b_j`, и каждый символ из строк `a` или `b` входит не более чем в одну пару.
Во входном файле содержатся две строки одинаковой длины, состоящие только из прописных латинских букв. Длина строк не превосходит 100 символов.
В выходной файл вывести одно число – число соответствий между строками.
Пример ввода
ABCBB
BADDBA
 5. Город-лабиринт
5. Город-лабиринт
Ограничения: время – 500ms/1000ms, память – 32MiB Ввод: input.txt или стандартный ввод Вывод: output.txt или стандартный вывод 
Послать решение Blockly Посылки Темы Где Обсудить (0)
В небольшом городе, имеющем квадратную форму, дорожные службы создали сложную сеть дорог и берут большие штрафы за нарушение правил движения. Путешественник хочет пересечь этот город, не нарушая правил движения. Для этого он купил на бензоколонке карту города и ввел ее в бортовой компьютер. Путешественник въезжает в город с запада по шоссе в северо-западный угол города и должен выехать по шоссе, ведущему на восток, из юго-восточного угла. Напишите программу, которая поможет путешественнику найти кратчайший путь в городе-лабиринте.
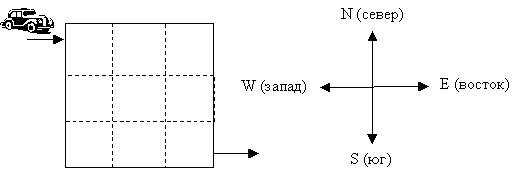
Во входном файле в первой строке содержится число `n` (`2\ ≤\ n\ ≤\ 20`) – размеры города. Далее следует `n` строк по n символов в каждой строке – информация о перекрестках. В городе существует всего три вида перекрестков. На перекрестке первого типа, обозначаемого во входном файле символом '+' (плюс), запрещены любые повороты, и необходимо продолжать движение в том же направлении. На перекрестке второго типа, обозначаемого символом '|' (вертикальная черта), при движении с запада на восток или с востока на запад нужно обязательно повернуть на север или на юг, а при движении с севера на юг или с юга на север – продолжить движение в том же направлении. На перекрестке третьего типа, обозначаемого символом '-' (минус), при движении с юга на север или с севера на юг нужно обязательно повернуть на запад или на восток, а при движении с востока на запад или с запада на восток – продолжить движение в том же направлении.
В выходной файл вывести кратчайший путь от первого перекрестка до выезда из города. Для каждого перекрестка, который встретится на пути путешественника, нужно указать направление дальнейшего движения – N (север), S (юг), W (запад) или E (восток). Если проехать через город без нарушения правил невозможно, то вывести сообщение "IMPOSSIBLE".
Пример ввода
3
-|+
|-|
-++
Вывод для примера
ESWSEEE
 Задачи 2 лиги областной олимпиады школьников по информатике 2002
Задачи 2 лиги областной олимпиады школьников по информатике 2002 1. Числа Фибоначчи
1. Числа Фибоначчи Модулярная арифметика
Модулярная арифметика

 2. Холмы и равнины
2. Холмы и равнины Реализация заданного алгоритма
Реализация заданного алгоритма

 3. Дроби
3. Дроби Алгоритм Эвклида
Алгоритм Эвклида

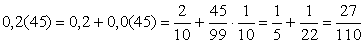 .
. 4. Число соответствий
4. Число соответствий Полный перебор
Полный перебор

 5. Город-лабиринт
5. Город-лабиринт Поиск в ширину (BFS)
Поиск в ширину (BFS)



 Начало
Начало Соревнования
Соревнования