Задачи 1 лиги личного первенства областной олимпиады школьников по информатике 2003

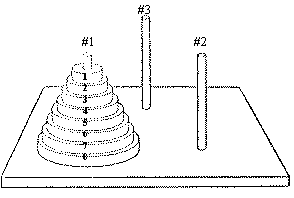
Головоломку "Ханойская башня" придумал французский математик Эдуард Люка. Игрушка, продававшаяся в 1883 году, состояла из 8 колец. Задача состоит в том, чтобы перенести за наименьшее число ходов пирамиду из колец разного диаметра с одного колышка на другой, используя третий колышек как вспомогательный. За один раз разрешается переносить только одно кольцо, причем нельзя класть кольцо большего диаметра на кольцо меньшего диаметра. В описании к игре рассказывалось о мифической "Пирамиде браминов", состоявшей из 64 золотых колец, в храме индийского города Бенареса. Каждый ход жрецы сопровождают молитвами, помогающими им действовать в правильном направлении. По преданию, как только жрецы храма сделают последний ход, грянет гром, храм рассыплется в пыль, погаснут звезды и наступит конец света. Так как для завершения работы жрецам потребуется `10^14` лет, то можно считать это предсказание верным: не только храм за такое время превратится в пыль, но и по расчетам физиков все звезды превратятся в холодные тела или черные дыры.

Решается головоломка достаточно просто. Например, чтобы переместить пирамиду из 8 дисков с колышка #1 на #2, используя #3, нужно

Наименьшее количество ходов для решения головоломки из `N` дисков равно `2^N-1`.

Напишите программу, которая по количеству дисков и числу сделанных ходов в минимальной последовательности ходов, требующихся для решения головоломки, определяет размещение дисков по колышкам после указанного хода. Диски пронумерованы от 1 (самый маленький) до `N` (самый большой). Требуется перенести диски с колышка #1 на колышек #2.

Во входном файле содержится две строки. В первой строке содержится целое число `N` – число дисков (`1\ ≤\ N\ ≤\ 100`). Во второй строке содержится целое число `K` – число выполненных ходов (`0\ ≤\ K\ ≤\ 2^N-1`).

В выходной файл вывести три строки – в `j`-й строке содержится количество и номера дисков, начиная с меньшего диска, на `j`-ом колышке, разделенные пробелом.

8
19

3 6 7 8
2 3 4
3 1 2 5

В романе математика Ч. Хинтона "Эпизод из жизни Флатландии" описывается любопытный мир без третьего измерения. В плоском мире действует такая же гравитация, как у нас, и вокруг плоского солнца вращаются плоские круглые планеты. На единственном континенте планеты Астрия живут два враждебных народа – унэйцы и сцинтийцы. Сцинтийцы используют для нападения десантные корабли, которые всегда летают по прямой линии с фиксированной скоростью (двигатель корабля компенсирует действие гравитации). Для защиты рубежей своей страны унэйские ученые разработали систему ПВО "Квадрат". Система стреляет неуправляемыми снарядами под фиксированным углом и с одинаковой стартовой скоростью. Можно управлять только временем запуска снарядов.

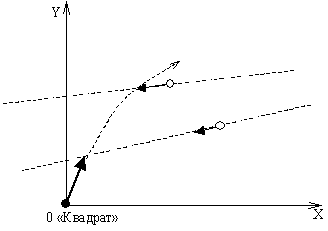
Напишите программное обеспечение для управления установкой "Квадрат".

На вход программы передается информация об обнаруженных целях в момент времени 0 – координаты целей относительно системы "Квадрат", скорость и направление полета. Программа должна для каждой цели определить время запуска снаряда, причем цель должна быть сбита до момента ее приземления на поверхность планеты. При вычислениях будем считать, что сопротивление воздуха отсутствует, поверхность планеты плоская, а все цели являются точечными. Система координат в задаче привязана к пусковой установке. Ось `X` соответствует поверхности планеты. Ускорение свободного падения на планете Астрия равно 10 м/с`^2`.

Во входном файле в первой строке содержится два целых числа через пробел – начальная скорость снаряда `U` при запуске в м/с и угол запуска `P` в градусах (`10\ ≤\ U\ ≤\ 1000`, `0\ <\ P\ <\ 90`). Во второй строке содержится одно целое число – количество обнаруженных целей `N` (`0\ <\ N\ ≤\ 20`). Далее следует `N` строк, в каждой строке содержится по четыре целых числа, разделенных пробелами – координаты цели `X_i` и `Y_i` в метрах, скорость цели `V_i` в м/c и направление движения цели `D_i` в градусах (`1\ ≤\ i\ ≤\ N`, `0\ <\ X_i\ ≤\ 1000`, `0\ <\ Y_i\ ≤\ 1000`, `0\ <\ "Vi"\ ≤\ 1000`, `0\ ≤\ "Di"\ <\ 360`).

В выходной файл вывести `N` строк. В `i`-ой строке нужно вывести время запуска снаряда для поражения `i`-й цели в воздухе с 2 десятичными знаками или слово MISS, если цель поразить не удастся.

100 45
2
200 50 10 180
100 200 100 190

13.97
MISS

Крестьянин, возвращаясь с ярмарки, увидел на мосту странную картину. Какой-то человек сначала считал деньги в кошельке, затем бросал в реку несколько монеток, бежал на другой конец моста, снова считал деньги в кошельке, и опять бросал несколько монеток и шел на другой конец моста. Наконец, пересчитав свои деньги, он явно обрадовался и отправился в дальнейший путь.

- Что ты делал? Зачем ты бросал деньги в воду? – спросил крестьянин, догнав странного человека.

Видя, что свой секрет скрыть не удастся, человек рассказал, что мост волшебный, что, если бросить с моста ровно 29 копеек, то, как только перейдешь мост, количество рублей в оставшейся сумме денег превращаются в новой сумме в количество копеек, а копейки – в рубли, что, перейдя мост несколько раз, можно получить сумму, намного большую первоначальной.

- Самое важное – вовремя остановиться, – сказал человек и ушёл.

Крестьянин задумался, достал кошелек и пересчитал свои деньги. У него было 46 рублей 47 копеек. "29 копеек – не деньги, дай-ка попробую". После первого прохода у него получилось 18р.46к., после второго прохода – 17р.18к., а после третьего – 89р.16к. "Ух-ты! А еще больше можно получить?" – обрадовался крестьянин. После четвертого прохода у него стало 87р.88к., после пятого – 59р.87к., после шестого – 58р.59к., после седьмого – 30р.58к., после восьмого – 29р.30к., после девятого – 1р.29к., а после десятого осталась 1 копейка.

"Эх, дурачина, надо было после третьего раза остановиться!" – расстроился крестьянин.

Напишите программу, которая по начальной сумме денег у крестьянина определит оптимальное число проходов по мосту для получения наибольшей конечной суммы.

Во входном файле в первой строке содержится целое число `M` – количество копеек, которые нужно бросать с моста (`1\ ≤\ M\ ≤\ 50`). Во второй строке содержатся два целых числа `R` и `K` через пробел – начальная сумма денег у крестьянина, выраженная в рублях и копейках (`0\ ≤\ R\ ≤\ 99`, `0\ ≤\ K\ ≤\ 99`).

В выходной файл вывести наименьшее количество проходов по мосту для получения максимально возможной суммы.

29
46 47

3

Юный энтомолог изучает уровень интеллекта кузнечика, используя специальный полигон. Прямоугольный полигон был разделен на клетки размером 10x10 см и в каждой клетке был поставлен столбик из кубиков. Столбик может содержать от 0 до 9 кубиков. Все кубики имеют размер стороны 10 см.

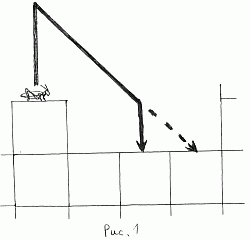
Кузнечик прыгает по следующим правилам. Кузнечик может прыгать только в направлениях, параллельных стенам полигона. Перед прыжком он становится точно в центр верхней грани столбика из кубиков и прыгает вертикально вверх на 20 см. Затем он планирует, используя крылья, в выбранном направлении, теряя по 10 см высоты на 10 см горизонтального полета. В любой момент он также может сложить крылья и спикировать вертикально вниз, как показано на рис. 1. 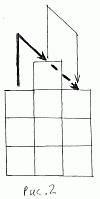Кузнечик не может пробивать кубики, поэтому, чтобы попасть с левого столбика на правый на рис. 2, ему потребуется два прыжка. Кузнечик не может также покинуть полигон.

Напишите программу, которая определит наименьшее число прыжков, требующееся кузнечику, чтобы добраться до заданной клетки.

Во входном файле в первой строке содержатся два целых числа `N` и `M` через пробел – размеры полигона в клетках (`1\ <\ N\ ≤\ 100`, `1\ <\ M\ ≤\ 100`). Во второй строке содержатся два целых числа `X_1` и `Y_1` через пробел – координаты начальной клетки (`1\ ≤\ X_1\ ≤\ N`, `1\ ≤\ Y_1\ ≤\ M`). В третьей строке содержатся два целых числа `X_2` и `Y_2` через пробел – координаты конечной клетки (`1\ ≤\ X_2\ ≤\ N`, `1\ ≤\ Y_2\ ≤\ M`). Далее следует `M` строк, содержащих по `N` целых чисел от 0 до 9, разделенных пробелами – высота столбика из кубиков в соответствующей клетке на полигоне. Первое число первой строки соответствует координате `(1,1)`, а последнее число последней строки – координате `(N,M)`.

В выходной файл в первой строке вывести целое число `K` – минимальное количество прыжков, которое потребуется кузнечику, чтобы добраться от начальной клетки до конечной. Далее следует `K+1` строка с координатами клеток – путь кузнечика, включая начальную и конечную клетку. Если возможно несколько вариантов, то нужно вывести любой (один) из них. Если добраться до конечной клетки невозможно, то вывести сообщение "IMPOSSIBLE" без кавычек.

3 3
2 1
3 3
3 0 3
2 0 4
1 0 5

7
2 1
2 3
1 3
1 2
1 1
3 1
3 2
3 3